Đề bài
Cho tam giác ABC vuông tại A, \(AC = 4cm,BC = 6cm.\) Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho \(BD = 9cm.\) Số đo góc ABD bằng bao nhiêu độ?
-
A.
80\(^0\).
-
B.
90\(^0\).
-
C.
95\(^0\).
-
D.
85\(^0\).
Phương pháp giải
Sử dụng kiến thức trường hợp đồng dạng thứ nhất của tam giác vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau.
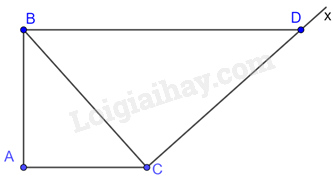
Tam giác ABC và tam giác CDB có:
\(\widehat A = \widehat {BCD} = {90^0},\frac{{AC}}{{BC}} = \frac{{BC}}{{BD}}\left( { = \frac{2}{3}} \right)\)
Do đó, \(\Delta ABC \backsim \Delta CDB\) nên \(\widehat {ABC} = \widehat {BDC}\)
Mà \(\widehat {BDC} + \widehat {CBD} = {90^0}\) nên \(\widehat {ABC} + \widehat {CBD} = {90^0}\) hay \(\widehat {ABD} = {90^0}\)
Đáp án : B