Cho tam giác ABC vuông tại A, \(AC = 4cm,BC = 6cm.\)Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho \(BD = 9cm.\) Diện tích tam giác ABD bằng:
-
A.
\(9\sqrt {20} c{m^2}\)
-
B.
\(\frac{9}{2}\sqrt {20} c{m^2}\)
-
C.
\(\sqrt {20} c{m^2}\)
-
D.
\(\frac{9}{4}\sqrt {20} c{m^2}\)
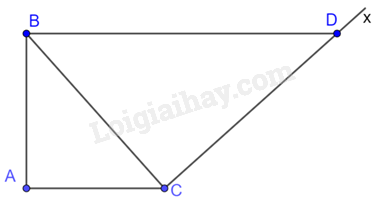
Tam giác ABC và tam giác CDB có:
\(\widehat A = \widehat {BCD} = {90^0},\frac{{AC}}{{BC}} = \frac{{BC}}{{BD}}\left( { = \frac{2}{3}} \right)\)
Do đó, \(\Delta ABC \backsim \Delta CDB\) nên \(\widehat {ABC} = \widehat {BDC}\)
Mà \(\widehat {BDC} + \widehat {CBD} = {90^0}\) nên \(\widehat {ABC} + \widehat {CBD} = {90^0}\) hay \(\widehat {ABD} = {90^0}\)
Do đó, tam giác ABD vuông tại B
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A có:
\(A{B^2} + A{C^2} = B{C^2}\)
\(A{B^2} = B{C^2} - A{C^2} = 20\)
\(AB = \sqrt {20} cm\)
Do tam giác ABD vuông tại B nên diện tích tam giác ABD là:
\(\frac{1}{2}AB.BD = \frac{1}{2}.\sqrt {20} .9 = \frac{9}{2}\sqrt {20} \left( {c{m^2}} \right)\)
Đáp án : B