Cho tam giác ABC vuông tại A, có AB = 3cm,AC = 4cm,AD là — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức về tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.

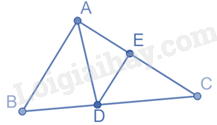
Kẻ DE vuông góc với AC tại E, khi đó DE là khoảng cách từ D đến AC

Lại có: AB vuông góc với AC nên DE//AB

Áp dụng định lý Pytago vào tam giác ABC vuông tại A có: \(B{C^2} = A{B^2} + A{C^2} = 25\) nên \(BC = 5cm\)

Xét tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{3}{4}\) nên \(BD = \frac{3}{4}DC\)

Ta có: \(BD + DC = BC\)

\(\frac{3}{4}DC + DC = 5\) nên \(DC = \frac{{20}}{7}cm\)

Tam giác ABC có DE//AB nên theo hệ quả của định lý Thalès ta có:

\(\frac{{DE}}{{AB}} = \frac{{DC}}{{BC}}\) hay \(\frac{{DE}}{3} = \frac{{\frac{{20}}{7}}}{5} = \frac{4}{7}\) nên \(DE = \frac{4}{7}.3 = \frac{{12}}{7}\left( {cm} \right)\)

Vì AD là đường phân giác của góc BAC nên \(\widehat {DAE} = \frac{1}{2}\widehat {BAC} = {45^0}\)

Mà tam giác DAE vuông tại E nên tam giác DAE vuông cân tại E. Do đó, \(DE = AE = \frac{{12}}{7}cm\)