Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 5{\rm{\;cm}}\) và \(BC = 13{\rm{\;cm}}\). Qua trung điểm \(M\) của \({\rm{AB}}\), vẽ một đường thẳng song song với \({\rm{AC}}\) cắt \({\rm{BC}}\) tại \({\rm{N}}\). Tính độ dài \({\rm{MN}}\).
-
A.
\(6\left( {{\rm{\;m}}} \right)\)
-
B.
\(7,5\left( {{\rm{\;m}}} \right)\)
-
C.
\(2,5\left( {{\rm{\;m}}} \right)\)
-
D.
\(10\left( {{\rm{\;m}}} \right)\)
Áp dụng định lí Pythagore vào \(\Delta {\rm{ABC}}\) vuông tại \({\rm{A}}\) để tính cạnh \({\rm{AC}}\).
Áp dụng định lí: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Từ đó suy ra \({\rm{MN}}\) là đường trung bình.
Đường trung bình của tam giác thì song song vơi cạnh thứ ba và bằng nửa cạnh ấy.
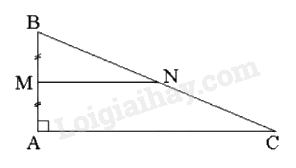
Áp dụng định lí Pythagore vào \(\Delta {\rm{ABC}}\) vuông tại \({\rm{A}}\) có: \({\rm{B}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2}\) hay \({\rm{A}}{{\rm{C}}^2} = {\rm{B}}{{\rm{C}}^2} - {\rm{A}}{{\rm{B}}^2} = {13^2} - {5^2} = 144\) suy ra \({\rm{AC}} = 12{\rm{\;cm}}\)
Xét \(\Delta {\rm{ABC}}\) có \({\rm{MA}} = {\rm{MB}}\) (theo gt); \({\rm{MN}}//{\rm{AC}}\) (theo gt) nên \({\rm{NB}} = {\rm{NC}}\)
Do đó \({\rm{MN}}\) là đường trung bình của \(\Delta {\rm{ABC}}\) suy ra \({\rm{MN}} = \frac{1}{2}{\rm{AC}}\) hay \({\rm{MN}} = \frac{1}{2} \cdot 12 = 6\left( {{\rm{\;cm}}} \right)\).
Đáp án A.
Đáp án : A