Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = — Không quảng cáo

a) Độ dài BH là 7,2cm.

b) \(\sin DAC = \frac{{\sqrt 2 }}{2}\).

c) \(\tan HAD \approx 7,12\).

d) \(AH = BC.\sin B.\cos B\) .

a) Chứng minh $\Delta ABC\backsim \Delta HBA$ suy ra \(\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\) và tính BH.

b) Dựa vào tính chất của tia phân giác của một góc, tính sin của góc đó.

c) \(\widehat {BAD} = \widehat {BAH} + \widehat {HAD}\), tính góc \(\widehat {BAD},\widehat {BAH}\) suy ra \(\widehat {HAD}\), từ đó tính được \(\tan HAD\).

d) Biến đổi \(BC.\sin B.\cos B\) thành AH.

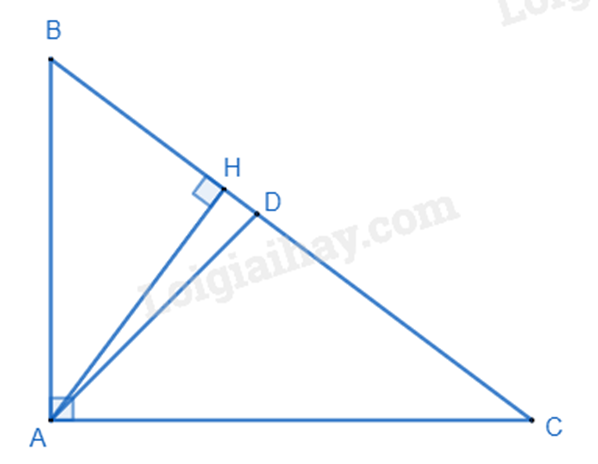
a) Xét tam giác ABC và tam giác HBA có:

\(\widehat A = \widehat H\left( { = 90^\circ } \right)\)

\(\widehat B\) chung

Suy ra $\Delta ABC\backsim \Delta HBA$ (g.g)

Suy ra \(\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\), do đó \(BH = \frac{{A{B^2}}}{{BC}} = \frac{{{{12}^2}}}{{20}} = 7,2\left( {cm} \right)\).

Vậy khẳng định a) đúng .

b) Vì AD là tia phân giác của góc BAC nên \(\widehat {BAD} = \widehat {DAC} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.90^\circ  = 45^\circ \).

Ta có \(\sin DAC = \sin 45^\circ  = \frac{{\sqrt 2 }}{2}\).

Vậy khẳng định b) đúng .

c) Xét tam giác BHA, ta có:

\(\sin BAH = \frac{{BH}}{{AB}} = \frac{{7,2}}{{12}} = \frac{3}{5}\) suy ra \(\widehat {BAH} \approx 37^\circ \)

Ta có: \(\widehat {BAD} = \widehat {BAH} + \widehat {HAD}\) suy ra \(\widehat {HAD} = \widehat {BAD} - \widehat {BAH} \approx 45^\circ  - 37^\circ  = 8^\circ \).

Suy ra \(\tan HAD = \tan 8^\circ  \approx 0,14\left( {cm} \right)\).

Vậy khẳng định c) sai .

d) Ta có: \(BC.\sin B.\cos B = BC.\frac{{AH}}{{AB}}.\frac{{AB}}{{BC}} = AH\).

Vậy khẳng định d) đúng .

Đáp án a) Đ, b) Đ, c) S, d) Đ.