Cho tam giác ABC vuông tại A có M là trung điểm của BC. Gọi I là hình chiếu của M trên AC. Chọn đáp án đúng.
-
A.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{2}\)
-
B.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{3}\)
-
C.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{4}\)
-
D.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{2}{3}\)
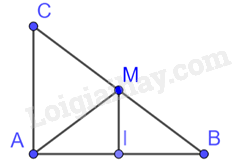
Tam giác ABC vuông tại A có AM là trung tuyến nên \(AM = MB = \frac{1}{2}BC\)
Do đó, tam giác AMB cân tại M. Do đó, MI là đường cao đồng thời là đường trung tuyến nên \(AI = \frac{1}{2}AB \Rightarrow \frac{{AI}}{{AB}} = \frac{1}{2}\)
Tam giác ABC có: M là trung điểm của CB, I là trung điểm của AB nên MI là đường trung bình của tam giác ABC nên \(\frac{{MI}}{{AC}} = \frac{1}{2}\)
Tam giác ABC và tam giác AIM có:
\(\widehat {BAC} = \widehat {MIA} = {90^0},\frac{{AI}}{{AB}} = \frac{{MI}}{{AC}}\left( { = \frac{1}{2}} \right)\) nên \(\Delta IAM \backsim \Delta ABC\)
Do đó, \(\frac{{{S_{ABC}}}}{{{S_{AMI}}}} = {\left( {\frac{{MI}}{{AC}}} \right)^2} = \frac{1}{4}\)
Đáp án : C