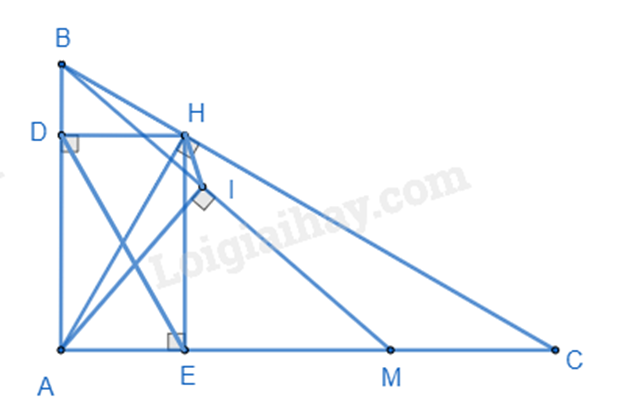
Cho tam giác ABC vuông tại A, đường cao AH. A Biết AB = 2 — Không quảng cáo

Phương pháp giải

a) Vận dụng các kiến thức về hệ thức lượng trong tam giác vuông để giải tam giác.

b) Chứng minh $\Delta BHD\backsim \Delta HAD\left( g.g \right)$ suy ra \(BD.DA = D{H^2}\)

Chứng minh $\Delta CHE\backsim \Delta HAE\left( g.g \right)$ suy ra \(CE.AE = H{E^2}\).

\(BD.DA + CE.AE = D{H^2} + H{E^2}\)

Chứng minh tứ giác ADHE là hình chữ nhật nên \(AH = DE\).

Áp dụng định lí Pythagore vào tam giác DHE vuông tại H, ta có: \(D{H^2} + H{E^2} = D{E^2}\).

Suy ra \(D{H^2} + H{E^2} = A{H^2}\)

Từ đó ta có \(BD.DA + CE.AE = A{H^2}\) (đpcm)

c) Chứng minh $\Delta BIA\backsim \Delta BAM\left( g.g \right)$ suy ra \(BI.BM = A{B^2}\).

Chứng minh $\Delta BHA\backsim \Delta BAC\left( g.g \right)$ suy ra \(BH.BC = A{B^2}\).

Do đó \(BI.BM = BH.BC\) hay \(\frac{{BI}}{{BC}} = \frac{{BH}}{{BM}}\).

Chứng minh $\Delta BHI\backsim \Delta BMC$ suy ra \(\frac{{HI}}{{MC}} = \frac{{BI}}{{BC}}\).

Dựa vào kiến thức về tỉ số lượng giác, ta có: \(\sin \widehat {AMB} = \frac{{AB}}{{BM}}\); \(\sin \widehat {ACB} = \frac{{AB}}{{BC}}\).

Biến đối \(\sin \widehat {AMB}.\sin \widehat {ACB} = \frac{{AB}}{{BM}}.\frac{{AB}}{{BC}} = \frac{{A{B^2}}}{{BM.BC}} = \frac{{BI}}{{BC}} = \frac{{HI}}{{CM}}\). Ta được điều phải chứng minh.

a) Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore trong tam giác, ta có:

\(B{C^2} = A{B^2} + A{C^2} = {\left( {2\sqrt 3 } \right)^2} + {6^2} = 48\) suy ra \(BC = \sqrt {48}  = 4\sqrt 3 \left( {cm} \right)\)

Ta có: \(\sin B = \frac{{AC}}{{BC}} = \frac{6}{{4\sqrt 3 }} = \frac{{\sqrt 3 }}{2}\) suy ra \(\widehat B = 60^\circ \).

\(\widehat C = 90^\circ  - \widehat B = 90^\circ  - 60^\circ  = 30^\circ \).

Vậy \(BC = 4\sqrt 3 cm;\widehat B = 60^\circ ;\widehat C = 30^\circ \).

b) Xét tam giác BHD và tam giác HAD có:

\(\widehat {BDH} = \widehat {HDA}\left( { = 90^\circ } \right)\)

\(\widehat {BHD} = \widehat {HAD}\) (cùng phụ với \(\widehat {DBH}\))

suy ra $\Delta BHD\backsim \Delta HAD\left( g.g \right)$ nên \(\frac{{BD}}{{DH}} = \frac{{DH}}{{DA}}\). Do đó  \(BD.DA = D{H^2}\). (1)

Xét tam giác CHE và tam giác HAE có:

\(\widehat {CEH} = \widehat {HEA}\left( { = 90^\circ } \right)\)

\(\widehat {CHE} = \widehat {HAE}\) (cùng phụ với \(\widehat {C}\))

suy ra $\Delta CHE\backsim \Delta HAE\left( g.g \right)$ nên \(\frac{{CE}}{{HE}} = \frac{{HE}}{{AE}}\). Do đó \(CE.AE = H{E^2}\). (2)

Từ (1) và (2) suy ra \(BD.DA + CE.AE = D{H^2} + H{E^2}\) (3).

Vì tứ giác ADHE có \(\widehat {DAE} = \widehat {ADH} = \widehat {AEH} = 90^\circ \) nên tứ giác ADHE là hình chữ nhật. Do đó \(AH = DE\).

Áp dụng định lí Pythagore vào tam giác DHE vuông tại H, ta có: \(D{H^2} + H{E^2} = D{E^2}\). Suy ra \(D{H^2} + H{E^2} = A{H^2}\) (4)

Từ (3) và (4) suy ra \(BD.DA + CE.AE = A{H^2}\) (đpcm)

c) Xét tam giác BIA và tam giác BAM có:

\(\widehat {BIA} = \widehat {BAM}\left( { = 90^\circ } \right)\)

\(\widehat B\) chung

suy ra $\Delta BIA\backsim \Delta BAM\left( g.g \right)$ nên \(\frac{{BI}}{{AB}} = \frac{{AB}}{{BM}}\). Do đó \(BI.BM = A{B^2}\).

Xét tam giác BHA và tam giác BAC có:

\(\widehat {BHA} = \widehat {BAC}\left( { = 90^\circ } \right)\)

\(\widehat B\) chung

suy ra $\Delta BHA\backsim \Delta BAC\left( g.g \right)$ nên \(\frac{{BH}}{{AB}} = \frac{{AB}}{{BC}}\). Do đó \(BH.BC = A{B^2}\).

Từ đó ta có \(BI.BM = BH.BC\) suy ra \(\frac{{BI}}{{BC}} = \frac{{BH}}{{BM}}\).

Xét tam giác BHI và tam giác BMC có:

\(\widehat B\) chung

\(\frac{{BI}}{{BC}} = \frac{{BH}}{{BM}}\) (cmt)

nên $\Delta BHI\backsim \Delta BMC$ (c.g.c) suy ra \(\frac{{HI}}{{MC}} = \frac{{BI}}{{BC}}\).

Xét tam giác AMB vuông tại A, ta có: \(\sin \widehat {AMB} = \frac{{AB}}{{BM}}\).

Xét tam giác ABC vuông tại A, ta có: \(\sin \widehat {ACB} = \frac{{AB}}{{BC}}\).

Suy ra \(\sin \widehat {AMB}.\sin \widehat {ACB} = \frac{{AB}}{{BM}}.\frac{{AB}}{{BC}} = \frac{{A{B^2}}}{{BM.BC}} = \frac{{BI.BM}}{{BM.BC}} = \frac{{BI}}{{BC}} = \frac{{HI}}{{CM}}\).

Vậy \(\sin \widehat {AMB}.\sin \widehat {ACB} = \frac{{HI}}{{CM}}\) (đpcm).