Cho tam giác ABC vuông tại A, đường cao AH chia đoạn BC — Không quảng cáo

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ ba của tam giác vuông: Nếu tam vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

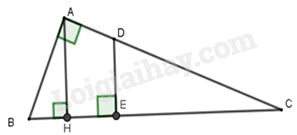
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.

Tam giác AHC và tam giác ABC có: \(\widehat {AHC} = \widehat {BAC} = {90^0},\widehat C\;chung.\) Do đó, \(\Delta ACH \backsim \Delta BCA\)

Ta có: \({S_{DEC}} = \frac{1}{2}{S_{ABC}}\left( 1 \right)\) , \(\frac{{{S_{AHC}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}HC.AH}}{{\frac{1}{2}BC.AH}} = \frac{{HC}}{{BC}} = \frac{{18}}{{25}} \Rightarrow {S_{AHC}} = \frac{{18}}{{25}}{S_{ABC}}\left( 2 \right)\)

Từ (1) và (2) ta có: \({S_{DEC}}:{S_{AHC}} = \frac{1}{2}:\frac{{18}}{{25}} = \frac{{25}}{{36}} = {\left( {\frac{5}{6}} \right)^2}\left( 3 \right)\)

Tam giác DEC và tam giác AHC có: \(\widehat {DEC} = \widehat {AHC} = {90^0},\widehat C\;chung\)

\(\Delta DEC \backsim \Delta AHC \Rightarrow \frac{{{S_{DEC}}}}{{{S_{AHC}}}} = {\left( {\frac{{EC}}{{HC}}} \right)^2}\left( 4 \right)\)

Từ (3) và (4) ta có: \(\frac{{EC}}{{HC}} = \frac{5}{6}\) \( \Rightarrow \) \(\frac{{EC}}{{18}} = \frac{5}{6} \Rightarrow EC = 15cm\)