Cho \(\Delta ABC\) vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E và HF vuông góc với AC tại F.
a) Chứng minh tứ giác AFHE là hình chữ nhật.
b) Trên tia đối của tia FH lấy điểm M sao cho FH = FM. Trên tia đối của tia EH lấy điểm N sao cho EH = EN. Chứng minh tứ giác AEFM là hình bình hành.
c) Chứng minh A, M, N thẳng hàng.
a) Chứng minh tứ giác AFHE có 3 góc vuông nên là hình chữ nhật.
b) Chứng minh tứ giác AEFM có một cặp cạnh đối song song và bằng nhau nên là hình bình hành.
c) Chứng minh AN và AM cùng song song với EF.
Dựa vào tiên đề Euclid thì A, M, N thẳng hàng.
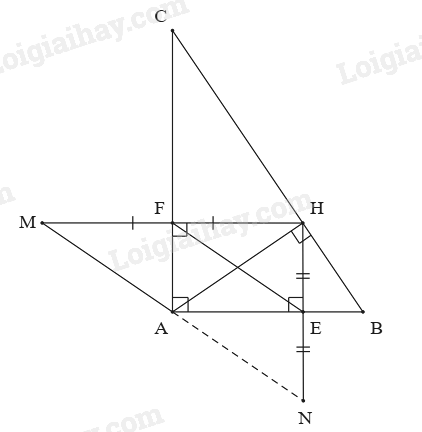
a) Xét tứ giác AFHE có:
\(\widehat A = \widehat E = \widehat F = 90^\circ \) (vì \(\Delta ABC\) vuông tại A, \(HE \bot AB\), \(HF \bot AC\))
Suy ra tứ giác AFHE là hình chữ nhật. (đpcm)
b) Vì FH // AE (do tứ giác AFHE là hình chữ nhật) nên MF // AE (vì F thuộc MH) (1)
Ta có FH = AE (do tứ giác AFHE là hình chữ nhật)
Mà FH = FM (giả thiết) suy ra AE = MF (2)
Từ (1) và (2) suy ra tứ giác AEFM là hình bình hành. (đpcm)
c) Vì AF = EH (do tứ giác AFHE là hình chữ nhật) nên AF // NE (vì E thuộc NH) (3)
Ta có AF = EH (do tứ giác AFHE là hình chữ nhật)
Mà HE = EN (gt) nên AF = NE (4)
Từ (3) và (4) suy ra tứ giác AFEN là hình bình hành.
Do đó AN // EF.
Mặt khác, AM // EF (vì tứ giác AEFM là hình bình hành)
Theo tiên đề Euclid thì A, M, N thẳng hàng. (đpcm)