Đề bài
Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
-
A.
\(2AC = CH.BC\)
-
B.
\(A{C^2} = \frac{1}{2}CH.BC\)
-
C.
\(A{C^2} = CH.BC\)
-
D.
\(A{C^2} = 2CH.BC\)
Phương pháp giải
Sử dụng kiến thức trường hợp đồng dạng thứ ba của tam giác vuông: Nếu tam vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
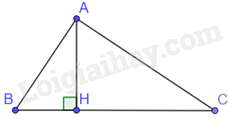
Tam giác ACH và tam giác CBA có: \(\widehat {AHC} = \widehat {BAC} = {90^0},\widehat C\;chung\)
Do đó, \(\Delta ACH \backsim \Delta BCA(g.g) \Rightarrow \frac{{AC}}{{BC}} = \frac{{CH}}{{AC}} \Rightarrow A{C^2} = CH.BC\)
Đáp án : C