Cho tam giác ABC vuông tại A. Gọi O là trung điểm của AC — Không quảng cáo

Phương pháp giải

a) Chứng minh tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

b) Chứng minh AO là đường trung bình của tam giác BED nên $AO = \frac{1}{2}ED$.

Mà O là trung điểm của AC nên $AO = \frac{1}{2}AC \Rightarrow AC = DE$.

c) Áp dụng tính chất của đường phân giác và định lí Thales đảo để chứng minh MN // AC.

Gọi F là giao điểm của BO và MN.

Dựa vào hệ quả của định lí Thales để suy ra MF = FN để được đpcm.

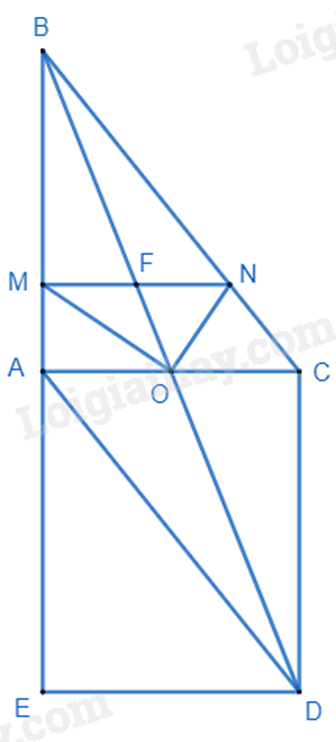
a) Xét tứ giác ABCD có:

O là trung điểm của AC

O là trung điểm của BD.

$AC \cap BD = O$

$\Rightarrow$ ABCD là hình bình hành. (đpcm)

b) Xét tam giác BED có:

A là trung điểm của BE

O là trung điểm của BD

$\Rightarrow$ AO là đường trung bình của tam giác BED.

$\Rightarrow AO = \frac{1}{2}ED$

Mà $AO = \frac{1}{2}AC$ (O là trung điểm của AC)

$\Rightarrow AC = ED$ (đpcm)

c) Áp dụng tính chất của đường phân giác, ta có:

OM là tia phân giác của $\widehat {AOB}$ $\Rightarrow \frac{{AO}}{{AM}} = \frac{{OB}}{{BM}} \Rightarrow \frac{{AO}}{{OB}} = \frac{{AM}}{{BM}}$

ON là tia phân giác của $\widehat {BOC}$ $\Rightarrow \frac{{OC}}{{CN}} = \frac{{OB}}{{BN}} \Rightarrow \frac{{OC}}{{OB}} = \frac{{CN}}{{BN}}$

Mà $AO = OC$ (gt)

$\Rightarrow \frac{{AM}}{{BM}} = \frac{{CN}}{{BN}}$$\Rightarrow MN//AC$ (định lí Thales đảo) (đpcm)

Gọi F là giao điểm của MN và BO.

Vì MN // AC nên áp dụng hệ quả của định lí Thales vào:

$\Delta AOB$ có: $\frac{{BF}}{{BO}} = \frac{{MF}}{{AO}}$

$\Delta BOC$ có: $\frac{{BF}}{{BO}} = \frac{{NF}}{{OC}}$

$\Rightarrow \frac{{MF}}{{AO}} = \frac{{NF}}{{OC}} \Rightarrow \frac{{MF}}{{NF}} = \frac{{AO}}{{OC}} = 1 \Rightarrow MF = NF$ hay F là trung điểm của MN $\Rightarrow$ BO đi qua trung điểm của MN. (đpcm)