Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ \(KD \bot AC\left( {D \in BC} \right)\). Chọn câu đúng.
-
A.
\(\Delta AHD = \Delta AKD\)
-
B.
$AD$ là đường trung trực của đoạn thẳng $HK.$
-
C.
\(AD\) là tia phân giác của góc \(HAK.\)
-
D.
Cả A, B, C đều đúng.
+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông
+ Sử dụng tính chất hai tam giác bằng nhau để chứng minh \(AD\) là tia phân giác của góc \(HAK.\)
+ Sử dụng định lý về đường trung trực để chỉ ra $AD$ là đường trung trực của đoạn thẳng $HK.$
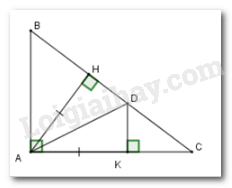
Xét tam giác vuông \(AHD\) và tam giác vuông \(AKD\) có
+ \(AH = AK\,\left( {gt} \right)\)
+ \(AD\) chung
Suy ra \(\Delta AHD = \Delta AKD\left( {ch - cgv} \right)\) nên A đúng
Từ đó ta có \(HD = DK;\,\widehat {HAD} = \widehat {DAK}\) suy ra \(AD\) là tia phân giác góc \(HAK\) nên C đúng.
Ta có \(AH = AK\left( {gt} \right)\) và \(HA = DK\left( {cmt} \right)\) suy ra \(AD\) là đường trung trực đoạn \(HK\) nên B đúng.
Vậy cả A, B, C đều đúng.
Đáp án : D