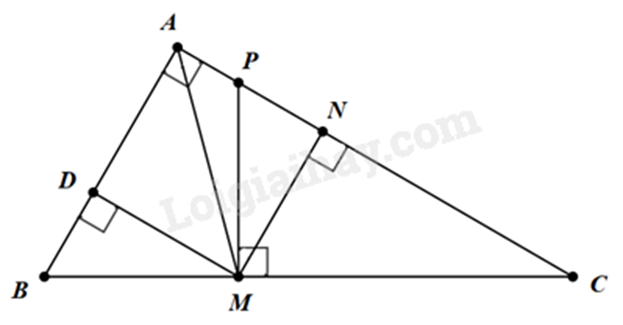
Cho tam giác ABC vuông tại A. Lấy điểm M sao cho AM là phân — Không quảng cáo

Phương pháp giải

a) Chứng minh tam giác MPC và tam giác ABC đồng dạng theo trường hợp góc – góc.

b) Dựa vào tính chất đường phân giác trong tam giác suy ra $\frac{{BM}}{{MC}} = \frac{{AB}}{{AC}}$.

Cộng cả hai vế với 1 để suy ra $\frac{{BC}}{{MC}} = \frac{{AB + AC}}{{AC}}$.

c) Kẻ MD vuông góc với AB tại D. Chứng minh $\Delta MPN = \Delta MBD\left( {ch - gn} \right)$ suy ra $MP = MB$

a) Xét $\Delta MPC$ và $\Delta ABC$ có:

$\widehat {PMC} = \widehat {BAC} = {90^0}$

$\widehat C$ chung

nên $\Delta MPC\backsim \Delta ABC\left( g.g \right)$ (đpcm)

b) Vì AM là tia phân giác của góc BAC nên $\frac{{BM}}{{MC}} = \frac{{AB}}{{AC}}$.

Cộng cả hai vế với 1 ta được:

$\begin{array}{l}\frac{{BM}}{{MC}} + 1 = \frac{{AB}}{{AC}} + 1\\\frac{{BM + MC}}{{MC}} = \frac{{AB + AC}}{{AC}}\\\frac{{BC}}{{MC}} = \frac{{AB + AC}}{{AC}}(dpcm)\end{array}$

c) Kẻ MD vuông góc với AB tại D.

Xét $\Delta ADM$ và $\Delta ANM$ có:

$\widehat D = \widehat N\left( { = {{90}^0}} \right)$

$\widehat {DAM} = \widehat {NAM}$ (AM là tia phân giác của góc BAC)

AM chung

Suy ra $\Delta ADM = \Delta ANM$ (cạnh huyền – góc nhọn)

Suy ra DM = NM (hai cạnh tương ứng)

Xét $\Delta MBD$ và $\Delta MPN$ có:

$\widehat D = \widehat N\left( { = {{90}^0}} \right)$

DM = NM (cmt)

$\widehat {BMD} = \widehat {PMN}$ (cùng phụ với $\widehat {DMP}$)

Suy ra $\Delta MBD = \Delta MPN$ (g.c.g)

Suy ra $MB = MP$ (hai cạnh tương ứng) (đpcm).