Đề bài
Cho tam giác ABC vuông tại A. Lấy một điểm M bất kì trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E. Khi đó:
-
A.
\(BM.BD + CM.CA = \frac{1}{2}B{C^2}\)
-
B.
\(BM.BD + 2CM.CA = B{C^2}\)
-
C.
\(BM.BD + CM.CA = B{C^2}\)
-
D.
\(BM.BD + CM.CA = 2B{C^2}\)
Phương pháp giải
Sử dụng kiến thức trường hợp đồng dạng thứ ba của tam giác vuông: Nếu tam vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
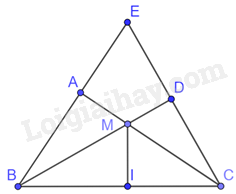
Kẻ MI vuông góc với BC tại I
Tam giác BIM và tam giác BDC có: \(\widehat {BIM} = \widehat {BDC} = {90^0},\widehat {MBC}\;chung\)
Do đó, \(\Delta BIM \backsim \Delta BDC \Rightarrow \frac{{BM}}{{BC}} = \frac{{BI}}{{BD}} \Rightarrow BM.BD = BC.BI\left( 1 \right)\)
Chứng minh tương tự ta có: \(\Delta ICM \backsim \Delta ACB \Rightarrow \frac{{CM}}{{BC}} = \frac{{CI}}{{CA}} \Rightarrow CM.CA = BC.CI\left( 2 \right)\)
Từ (1) và (2) ta có: \(BM.BD + CM.CA = BC.BI + BC.CI = BC\left( {BI + CI} \right) = B{C^2}\)
Đáp án : C