Cho tam giác ABC vuông tại $A,M$ là trung điểm của $AC. $ — Không quảng cáo

Phương pháp giải

- Sử dụng quan hệ giữa đường vuông góc với đường xiên

- Sử dụng tính chất của trung điểm

- Chứng minh \(\Delta ADM = \Delta CEM\) (ch - gn)

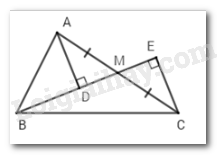
Vì \(\Delta ABM\) vuông tại $A$  (gt) nên \(BA < BM\) (quan hệ giữa đường vuông góc và đường xiên).

Mà \(BM = BD + DM \Rightarrow BA < BD + DM\left( 1 \right)\) .

Mặt khác, \(BM = BE - ME \Rightarrow BA < BE - ME\left( 2 \right)\)

Cộng hai vế của \(\left( 1 \right)\)và \(\left( 2 \right)\) ta được: \(2BA < BD + BE + MD - ME\left( 3 \right)\)

Vì $M$  là trung điểm của $AC$ (gt) \( \Rightarrow AM = MC\) (tính chất trung điểm)

Xét  tam giác vuông $ADM$  và tam giác vuông $CEM$  có:

\(AM = MC\left( {cmt} \right)\)

\(\widehat {AMD} = \widehat {EMC}\) (đối đỉnh)

\( \Rightarrow \Delta ADM = \Delta CEM\) (cạnh huyền – góc nhọn)

\( \Rightarrow MD = ME\left( 4 \right)\) (2 cạnh tương ứng)

Từ \(\left( 3 \right)\)và \(\left( 4 \right) \Rightarrow BD + BE > 2AB\)