Cho tam giác ABC vuông tại A và có đường phân giác BDD — Không quảng cáo

Phương pháp giải

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

Áp dụng Pythagore trong $\Delta ABC$ vuông tại $A$.

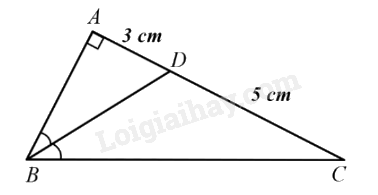
$\Delta ABC$ có $BD$ là tia phân giác của góc B suy ra $\frac{{AB}}{{BC}} = \frac{{AD}}{{DC}} = \frac{3}{5}$ hay $\frac{{AB}}{3} = \frac{{BC}}{5} = k(k \in \mathbb{R},k > 0)$.

Suy ra: $AB = 3k,BC = 5k$.

Áp dụng định lí Pythagore trong $\Delta ABC$ vuông tại $A$ ta có:

$B{C^2} = A{B^2} + A{C^2}$ hay ${(5k)^2} = {(3k)^2} + {(5 + 3)^2}$, suy ra $k = 2$

Từ đó ta có: $BC = 10{\rm{\;cm}}$.

Đáp án D.