Đề bài
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}.\) Gọi M, M’ lần lượt là trung điểm của BC và B’C’. Khi đó, tỉ số \(\frac{{AM}}{{A'M'}}\) bằng
-
A.
\(\frac{1}{3}\)
-
B.
\(\frac{1}{4}\)
-
C.
\(\frac{1}{2}\)
-
D.
\(2\)
Phương pháp giải
Sử dụng kiến thức trường hợp đồng dạng thứ hai của tam giác vuông: Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng.
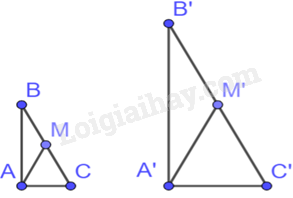
Tam giác ABC và tam giác A’B’C có: \(\widehat {BAC} = \widehat {B'A'C'} = {90^0},\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\)
Do đó, \(\Delta ABC \backsim \Delta A'B'C'\)
Suy ra: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{2}\)
Mà M là trung điểm của BC nên \(BC = 2AM\), M’ là trung điểm của B’C’ nên \(B'C' = 2A'M'\)
Do đó, \(\frac{{AM}}{{A'M'}} = \frac{1}{2}\)
Đáp án : C