Cho tam giác ABC vuông tại AAB — Không quảng cáo

Phương pháp giải

a) Chứng minh bắc cầu: $\left\{ {\begin{array}{*{20}{l}}{\widehat {DAB} + \widehat {BAM} = \widehat {DAM} = {{90}^0}\left( {do\,AM \bot AD} \right)}\\{\widehat {BAH} + \widehat {ABH} = \widehat {AHB} = {{90}^0}\left( {do\,AH \bot BC} \right)}\end{array}} \right.$

Chứng minh được: $\widehat {MBA} = \widehat {MAB}$

suy ra $\widehat {DAB} = \widehat {BAH}$ (cùng phụ với hai góc bằng nhau)

b) Sử dụng tính chất đường phân giác trong ${\rm{AB}}$ của tam giác ${\rm{ADH}}$

Sử dụng tính chất đường phân giác ngoài ${\rm{AC}}$ tại đỉnh ${\rm{A}}$ của tam giác ${\rm{ADH}}$.

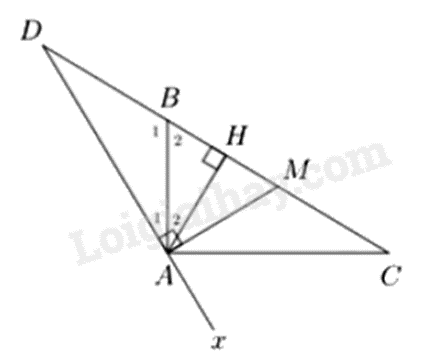
a) $\Delta ABC$ vuông tại $A$, đường trung tuyến $AM$ nên $AM = MB$ suy ra $\Delta AMB$ cân tại $M$

suy ra $\widehat {MBA} = \widehat {MAB}$ hay $\widehat {BAM} = \widehat {ABH}$

Ta có: $\left\{ {\begin{array}{*{20}{l}}{\widehat {DAB} + \widehat {BAM} = \widehat {DAM} = {{90}^0}\left( {do\,AM \bot AD} \right)}\\{\widehat {BAH} + \widehat {ABH} = \widehat {AHB} = {{90}^0}\left( {do\,AH \bot BC} \right)}\end{array}} \right.$

suy ra $\widehat {DAB} = \widehat {BAH}$ (cùng phụ với hai góc bằng nhau)

suy ra $AB$ là tia phân giác của $\widehat {DAH}$.

b) Vì $AB$ là tia phân giác của $\widehat {DAH}$ nên $\frac{{BH}}{{BD}} = \frac{{AH}}{{AD}}$ (tính chất đường phân giác)

Vì $AC \bot AB,\widehat {DAH}$ kề bù với $\widehat {HAx}$ nên $AC$ là tia phân giác $\widehat {HAx}$ suy ra $\frac{{CH}}{{CD}} = \frac{{AH}}{{AD}}$

Suy ra $\frac{{BH}}{{BD}} = \frac{{AH}}{{AD}} = \frac{{CH}}{{CD}}$. Do đó $BH \cdot CD = CH \cdot BD$.