Cho tam giác ABC vuông tại B, đường cao BH. Vẽ HE vuông góc — Không quảng cáo

Phương pháp giải

a) Sử dụng kiến thức về tỉ số lượng giác và hệ thức lượng của tam giác vuông để giải.

b) Chứng minh \(BE.AB = A{H^2} = B{C^2} - C{H^2}\)

c) Chứng minh \(\widehat {ABH} = \widehat C\).

Biểu diễn tỉ số lượng giác \(\tan ABH\) theo HE và BE.

Từ đó chứng minh \(BF = BE.\tan C\).

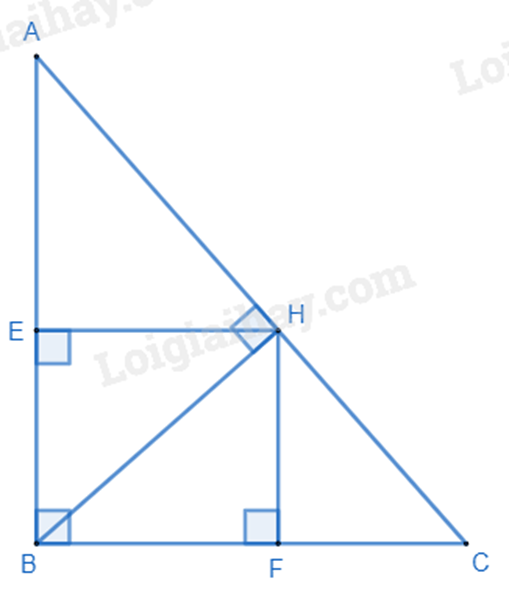
a) Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:

\(BC = \sqrt {A{C^2} - A{B^2}}  = \sqrt {{8^2} - {6^2}}  = 2\sqrt 7 \) (cm)

Áp dụng tỉ số lượng giác trong tam giác vuông ABC, ta có:

\(\sin ACB = \frac{{AB}}{{AC}} = \frac{6}{8} = \frac{3}{4}\)

Suy ra \(\widehat {ACB} \approx 49^\circ \)

Xét tam giác ABH vuông tại H, ta có:

\(\sin ACB = \frac{{BH}}{{BC}}\) suy ra \(\frac{{BH}}{{BC}} = \frac{3}{4}\)

Do đó \(BH = \frac{3}{4}BC = \frac{3}{4}.2\sqrt 7  = \frac{{6\sqrt 7 }}{4}\) (cm)

b) Xét tam giác BEH và tam giác BHA có:

\(\widehat {BEH} = \widehat {AHB}\left( { = 90^\circ } \right)\)

\(\widehat B\) chung

Suy ra $\Delta BEH\backsim \Delta BHA$ (g.g)

Suy ra \(\frac{{BE}}{{BH}} = \frac{{BH}}{{AB}}\), do đó \(BE.AB = B{H^2}\) (1)

Áp dụng định lí Pythagore vào tam giác BHC vuông tại H, ta có:

\(B{C^2} - H{C^2} = B{H^2}\) (2)

Từ (1) và (2) suy ra \(BE.BA = B{C^2} - H{C^2}\) (đpcm)

c) Ta có \(\widehat {ABH} = \widehat C\) (cùng phụ với \(\widehat A\))

Xét tứ giác BEHF có \(\widehat B = \widehat E = \widehat H = 90^\circ \) nên tứ giác BEHF là hình chữ nhật, suy ra \(HE = BF\).

Xét tam giác BHE, ta có: \(\tan HBE = \frac{{EH}}{{EB}}\) suy ra \(EH = BE.\tan HBE\)

Mà \(\widehat {HBE} = \widehat C\) và \(HE = BF\) (cmt) nên \(BF = BE.\tan C\) (đpcm).