Cho \(\Delta ABC\)vuông ở \(C\), có \(\widehat A = {60^o}\), tia phân giác của góc \(BAC\) cắt \(BC\) ở \(E\), kẻ \(EK\) vuông góc với \(AB\) (\(K\) thuộc \(AB\)), kẻ \(BD\) vuông góc với \(AE\) (\(D\) thuộc \(AE\))
Chứng minh:
a) \(AK{\rm{ }} = {\rm{ }}KB\);
b) \(AD{\rm{ }} = {\rm{ }}BC\)
Sử dụng tính chất tam giác cân và dấu hiệu nhận biết hai tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau.
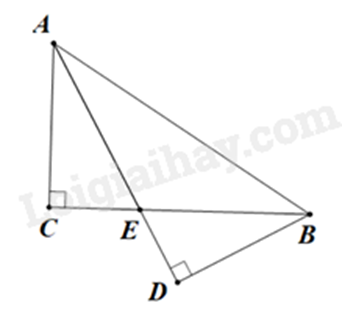
a) Ta có:
\(\widehat {EAB} = \frac{1}{2}\widehat {.BAC} = \frac{1}{2}{.60^{\rm{o}}} = {30^{\rm{o}}}\)(\(AE\) là phân giác của góc \(BAC\))
\(\widehat {ABC} = {90^{\rm{o}}} - \widehat {BAC} = {90^{\rm{o}}} - {60^{\rm{o}}} = {30^o}\)(Vì \(\Delta ABC\) vuông tại \(C\))
Suy ra \(\widehat {EAB} = \widehat {ABC}\)
\( \Rightarrow \Delta EAB\) cân tại \(E\)
Vậy \(EA{\rm{ }} = {\rm{ }}EB\)
* Xét \(\;\Delta EAK\)và \(\Delta EBK\)có:
\(\widehat {EKA} = \widehat {EKB} = {90^o}\)
\(EA{\rm{ }} = {\rm{ }}EB\) (chứng minh trên)
\(\widehat {EAB} = \widehat {ABC} = {30^o}\)
Suy ra \(\Delta EAK = \Delta EBK\)(cạnh huyền – góc nhọn)
Vậy \(KA = KB\;\)(2 cạnh tương ứng)
b) Xét \(\Delta CAB\) và \(\Delta DBA\)có:
\(\widehat {ACB} = \widehat {BDA} = {90^o}\)
\(AB\) chung
\(\widehat {ABC} = \widehat {BAD} = {30^o}\)
Suy ra \(\Delta CAB = \Delta DBA\)(cạnh huyền – góc nhọn)
Vậy\(BC = AD\) (2 cạnh tương ứng)