Cho tam giác OAB. Gọi C, D lần lượt là trung điểm của OA — Không quảng cáo

+ Nếu với mỗi điểm M thuộc hình $\mathcal{K}$, lấy điểm M’ thuộc tia OM sao cho $OM' = k.OM$ (hay $\frac{{OM'}}{{OM}} = k$) thì các điểm M’ đó tạo thành hình $\mathcal{K}'$. Ta nói hình $\mathcal{K}'$ đồng dạng phối cảnh với hình $\mathcal{K}$ theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.

+ Nếu $k > 1$ thì ta nói $\mathcal{K}'$ là hình phóng to của hình $\mathcal{K}$, nếu $k < 1$ thì ta nói $\mathcal{K}'$ là hình thu nhỏ của hình $\mathcal{K}$

+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.

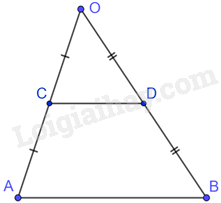
Vì C là trung điểm của OA nên $OC = \frac{1}{2}OA$

Vì D là trung điểm của OB nên $OD = \frac{1}{2}OB$

Mà O là giao điểm của AC và BD nên cạnh CD là hình đồng dạng phối cảnh của cạnh AB với tỉ số đồng dạng $k = \frac{1}{2}$ , tâm phối cảnh là điểm O.

Do đó, cạnh CD là hình đồng dạng của cạnh AB với tỉ số $k = \frac{1}{2}$

Suy ra, cả A, B đều đúng.