Cho tứ diện ABCD có ABC và BCD là các tam giác cân tại A và — Không quảng cáo

Phương pháp giải

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$.

+ Cho mặt phẳng (P). Xét một điểm M tùy ý trong không gian. Gọi d là đường thẳng đi qua điểm M và vuông góc với (P). Gọi M’ là giao điểm của đường thẳng d và mặt phẳng (P). Khi đó, điểm M’ được gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (P).

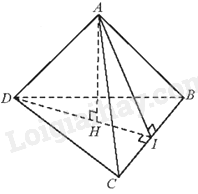
Vì tam giác ABC cân tại A nên AI là đường trung tuyến đồng thời là đường cao. Do đó, $AI \bot BC$.

Vì tam giác DBC cân tại D nên DI là đường trung tuyến đồng thời là đường cao. Do đó, $DI \bot BC$.

Ta có: $AI \bot BC$, $DI \bot BC$, DI và AI cắt nhau tại I và nằm trong mặt phẳng (AID) nên $BC \bot \left( {AID} \right)$. Mà $AH \subset \left( {ADI} \right) \Rightarrow AH \bot CB$

Lại có: $AH \bot DI$, DI và BC cắt nhau tại I và nằm trong mặt phẳng (BCD). Do đó, $AH \bot \left( {BCD} \right)$. Do đó, hình chiếu vuông góc của A trên mặt phẳng (BCD) là điểm H.

Đáp án B.