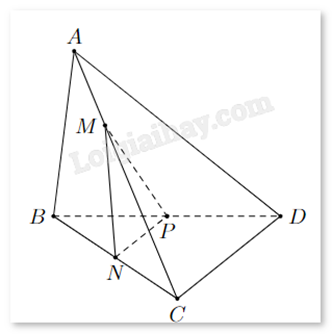
Cho tứ diện ABCD có N, P lần lượt là trung điểm của BC, BD — Không quảng cáo

- Định lý Thales.

- Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song là đường thẳng song song với hai đường thẳng đó.

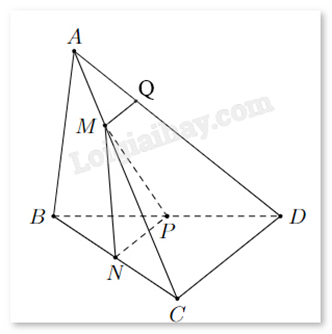
Xét tam giác BCD có N là trung điểm của BC, P là trung điểm của BD.

Khi đó, NP là đường trung bình của tam giác BCD, suy ra NP//CD.

Ta có $\left\{ {\begin{array}{*{20}{c}}{(MNP) \cap (ACD) = \{ M\} }\\\begin{array}{l}NP//CD\\NP \subset (MNP)\\CD \subset (ACD)\end{array}\end{array}} \right.$ nên giao tuyến của (MNP) và (ACD) là đường thẳng qua M song song với NP và CD. Gọi giao tuyến đó là d.

Mà $\left\{ {\begin{array}{*{20}{c}}{Q \in (MNP)}\\{Q \in AD \subset (ACD)}\end{array}} \right.$ nên $Q \in d$ và MQ//NP, MQ//CD.

Vì đã có MQ//NP nên để MNPQ là hình bình hành thì cần điều kiện MQ = NP.

Mà $NP = \frac{1}{2}CD$ nên cần $MQ = \frac{1}{2}CD$.

Xét tam giác ACD có $M \in AC$, $Q \in AD$ và MQ//CD.

Khi đó, $\frac{{AM}}{{AC}} = \frac{{MQ}}{{CD}}$ (định lý Thales đảo).

Vậy để MNPQ là hình bình hành thì $\frac{{AM}}{{AC}} = \frac{{MQ}}{{CD}} = \frac{1}{2} \Leftrightarrow AC = 2AM$.