Cho tứ diện ABCD, M thuộc đoạn AB, thiết diện của hình chóp — Không quảng cáo

Sử dụng tính chất: Nếu hai mặt phẳng $\left( \alpha  \right)$ và $\left( \beta  \right)$ có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của $\left( \alpha  \right)$ và $\left( \beta  \right)$ là đường thẳng đi qua M và song song với d và d’ để xác định thiết diện.

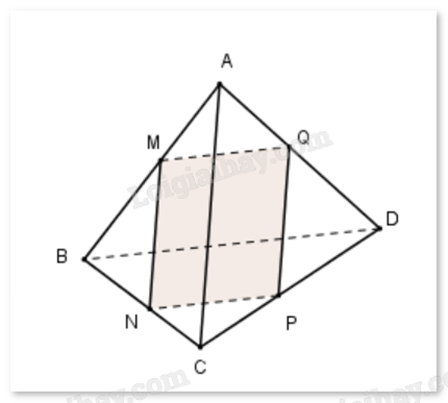
$\left\{ \begin{array}{l}M \in (\alpha ) \cap (ABC)\\(\alpha )//AC \subset (ABC)\end{array} \right.$ nên giao tuyến của $\left( \alpha  \right)$ và (ABC) là đường thẳng qua M và song song với AB, cắt BC tại N, suy ra MN//AC.

$\left\{ \begin{array}{l}N \in (\alpha ) \cap (BCD)\\(\alpha )//BD \subset (BCD)\end{array} \right.$ nên giao tuyến của $\left( \alpha  \right)$ và (BCD) là đường thẳng qua N và song song với BD, cắt CD tại P, suy ra NP//BD.

$\left\{ \begin{array}{l}P \in (\alpha ) \cap (ACD)\\(\alpha )//AC \subset (ACD)\end{array} \right.$ nên giao tuyến của $\left( \alpha  \right)$ và (ACD) là đường thẳng qua P và song song với AC, cắt AD tại Q, suy ra PQ//AC.

$\left\{ \begin{array}{l}P \in (\alpha ) \cap (ACD)\\(\alpha )//AC \subset (ACD)\end{array} \right.$ nên giao tuyến của $\left( \alpha  \right)$ và (ACD) là đường thẳng qua P và song song với AC, cắt AD tại Q, suy ra PQ//AC.

$\left\{ {\begin{array}{*{20}{c}}{(\alpha ) \cap (ABD) = MQ}\\{(\alpha )//BD \subset (ABD)}\end{array}} \right.$ nên MQ//BD.

Có: MN//PQ (cùng song song với AC), NP//MQ (cùng song song với BD) nên MNPQ là hình bình hành.

Vậy thiết diện cần tìm có 4 cạnh.