Đề bài
Cho tứ diện ABCD và điểm M thuộc miền trong tam giác ACD. Gọi I và J lần lượt là hai điểm trên cạnh BC và BD sao cho IJ sao cho IJ không song song với CD. Gọi H là giao điểm của IJ với CD, K là giao điểm của MH và AC. Giao tuyến của hai mặt phẳng (ACD) và (IJM) là:
-
A.
KI .
-
B.
KJ.
-
C.
HI.
-
D.
HM.
Phương pháp giải
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó và kí hiệu là d=(P)∩(Q).
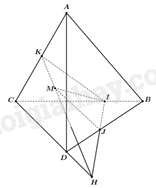
Ta có: M thuộc mặt phẳng (MIJ), M thuộc mặt phẳng (ACD) nên M là điểm chung của mặt phẳng (MIJ) và mặt phẳng (ACD).
Lại có: H∈CD⊂(ACD),H∈IJ⊂(IJM)⇒H∈(IJM)∩(ACD)
Vậy giao tuyến của hai mặt phẳng (ACD) và (IJM) là MH.
Đáp án : D