Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB và — Không quảng cáo

Phương pháp giải

Chứng minh tứ giác QMNP có hai đường chéo QN, PM giao nhau tại trung điểm O mỗi đường.

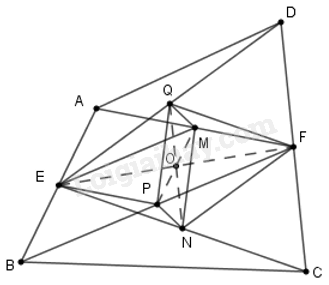
Nối EF; EP, FQ, EM, PM, QN. Gọi O là giao của QN và EF.

Xét tam giác CED ta có:  $\left\{ {\begin{array}{*{20}{c}}{FN = \frac{1}{2}DE = EQ}\\{FN//E{\rm{D}} \Rightarrow {\rm{FN//EQ}}}\end{array}} \right.$

⇒ NFQE là hình bình hành nên hai đường chéo QN và EF giao nhau tại trung điểm của mỗi đường. Suy ra O là trung điểm của QN và EF (1)

Xét tam giác ABF ta có:  $\left\{ {\begin{array}{*{20}{c}}{EM = \frac{1}{2}BF = PF}\\{EM//BF \Rightarrow EM//PF}\end{array}} \right.$

⇒ EMFB là hình bình hành nên hai đường chéo PM và EF giao nhau tại trung điểm của mỗi đường. Mà O là trung điểm của EF nên O cũng là trung điểm của PM (2)

Từ (1) và (2) suy ra: tứ giác QMNP có hai đường chéo QN, PM giao nhau tại trung điểm O mỗi đường nên QMNP là hình bình hành