Chu vi một tam giác là 16 cm, độ dài một cạnh tam giác là 6 — Không quảng cáo

Thiết lập hàm số biểu diễn diện tích của tam giác dựa vào công thức Heron. Lập bảng biến thiên tìm giá trị lớn nhất của hàm số đó.

Gọi x, y là độ dài hai cạnh còn lại của tam giác.

Ta có: x + y = 16 - 6 = 10 (x > 0, y > 0).

Diện tích tam giác là: \(S = \sqrt {p(p - 6)(p - x)(p - y)}  = \sqrt {8.2(8 - x)(8 - y)}  = 4\sqrt {(8 - x)(8 - y)} \).

Thay y = 10 – x, ta được: \(S = 4\sqrt {(8 - x)(x - 2)}  = 4\sqrt { - {x^2} + 10x - 16} \), \(x \in \left( {0;10} \right)\).

Đặt \(f(x) =  - {x^2} + 10x - 16\), ta có \(f'(x) =  - 2x + 10 = 0 \Leftrightarrow x = 5\).

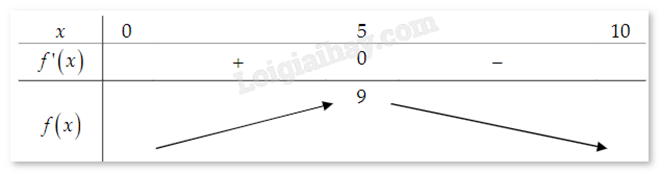
Từ bảng biến thiên, suy ra f(x) lớn nhất khi x = 5. Khi đó, diện tích tam giác cũng đạt giá trị lớn nhất là 12 \(c{m^2}\) khi x = 5.