Có thể em chưa biết: Cột cờ Hà Nội hay còn gọi Kỳ đài Hà Nội là một kết cấu dạng tháp được xây dựng cùng thời với thành Hà Nội dưới triều nhà Nguyễn (bắt đầu năm 1805, hoàn thành năm 1812). Kiến trúc cột cờ bao gồm ba tầng đế và một thân cột, được coi là một trong những biểu tượng của thành phố.
Đo chiều cao từ mặt đất đến đỉnh cột cờ của cột cờ Hà Nội (Kỳ đài Hà Nội), người ta cắm hai cọc bằng nhau MA và NB cao 1 m so với mặt đất. Hai cọc này song song, cách nhau 10 m và thẳng hàng so với tim cột cờ (như hình vẽ). Đặt giác kế đứng tại A và B để ngắm đến đỉnh cột cờ, người ta đo được các góc lần lượt là \(50^\circ 19'12''\) và \(43^\circ 16'\) so với đường song song mặt đất. Hãy tính chiều cao của cột cờ (làm tròn đến chữ số thập phân thứ hai)

Kẻ đoạn thẳng DC biểu diễn cột cờ, các cọc và cột cờ cùng vuông góc với mặt đất.
Kéo dài đoạn thẳng AB, cắt DC tại H.
Chứng minh AB = MN = 10m.
Biểu diễn \(\cot DAH\) và \(\cot DBH\) theo tỉ số lượng giác của tam giác vuông \(DAH\) và \(DBH\).
Từ đó tính chiều cao cột cờ DC theo DH và HC.
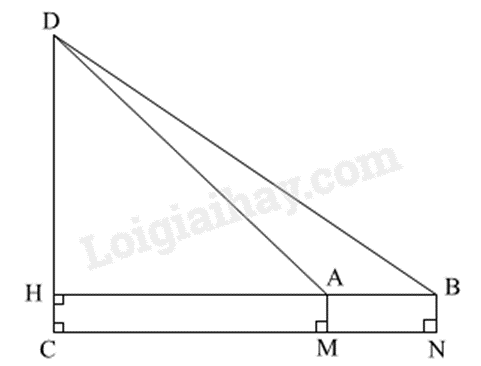
Kẻ DC là đoạn thẳng biểu diễn cột cờ, khi đó các cọc và cột cờ cùng vuông góc với mặt đất nên DC // AM // BN.
Xét tứ giác ABMN có AM // BN và AM = BN = 1 m nên ABMN là hình bình hành, suy ra \(AB = MN = 10m\), AB // MN.
Kéo dài AB cắt DC tại H, mà AB // MN nên AH // CN.
Mà \(DC \bot CN\) nên \(DH \bot HB\) hay \(\widehat {DHB} = 90^\circ \).
Xét tam giác DHA vuông tại H, ta có: \(\cot DAH = \frac{{AH}}{{DH}}\) suy ra \(AH = DH.\cot DAH\).
Xét tam giác DHB vuông tại H, ta có: \(\cot DBH = \frac{{BH}}{{DH}}\) suy ra \(BH = DH.\cot DBH\).
Ta có: \(AB = BH - AH\)
\(AB = DH.\cot DBH - DH.\cot DAH\)
\(AB = DH\left( {\cot DBH - \cot DAH} \right)\)
\(10 = DH\left( {\cot 43^\circ 16' - \cot 50^\circ 19'12''} \right)\)
\(DH = \frac{{10}}{{\cot 43^\circ 16' - \cot 50^\circ 19'12''}} \approx 42,96\left( m \right)\)
Tứ giác AMCH có \(\widehat M = \widehat C = \widehat H = 90^\circ \) nên tứ giác AMCH là hình chữ nhật, suy ra \(CH = AM = 1m\).
Vậy độ cao cột cờ DC là \(DC = DH + HC = 42,96 + 1 = 43,96\left( m \right)\).