Con lắc đạn đạo là thiết bị được sử dụng để đo tốc độ của viên đạn. Viên đạn được bắn vào một khối gỗ lớn treo lơ lửng bằng dây nhẹ, không dãn. Sau khi va chạm, viên đạn ghim vào trong gỗ. Sau đó, toàn bộ hệ khối gỗ và viên đạn chuyển động như một con lắc lên độ cao h như hình vẽ. Xét viên đạn có khối lượng \({m_1} = 5{\rm{ g}}\), khối gỗ có khối lượng \({m_2} = 1{\rm{ kg}}\) và \(h = 5{\rm{ cm}}\). Lấy \(g = 9,8{\rm{ m/}}{{\rm{s}}^2}\). Bỏ qua lực cản của không khí.
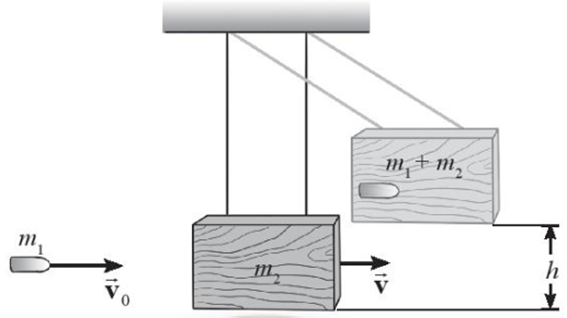
a) Trong thời gian va chạm động lượng được bảo toàn.
b) Động lượng hệ trước va cham: \(\overrightarrow {{p_t}} = m\overrightarrow {{v_0}} \)
c) Động lượng của hệ sau khi viên đạn đã găm vào khối gỗ: \(\overrightarrow {{p_s}} = (m + M)\overrightarrow V \)
d) Tốc độ ban đầu của viên đạn là \(V = 300m/s\)
a) Trong thời gian va chạm động lượng được bảo toàn.
b) Động lượng hệ trước va cham: \(\overrightarrow {{p_t}} = m\overrightarrow {{v_0}} \)
c) Động lượng của hệ sau khi viên đạn đã găm vào khối gỗ: \(\overrightarrow {{p_s}} = (m + M)\overrightarrow V \)
d) Tốc độ ban đầu của viên đạn là \(V = 300m/s\)
Vận dụng bảo toàn động lượng
a) Trong thời gian va chạm động lượng được bảo toàn.
Đúng
b) Động lượng hệ trước va cham: \(\overrightarrow {{p_t}} = m\overrightarrow {{v_0}} \)
Đúng
c) Động lượng của hệ sau khi viên đạn đã găm vào khối gỗ: \(\overrightarrow {{p_s}} = (m + M)\overrightarrow V \)
Đúng
d) Theo định luật bảo toàn động lượng \(\overrightarrow {{p_t}} = \overrightarrow {{p_s}} \, \Leftrightarrow (m + M)\overrightarrow V = m\overrightarrow {{v_0}} \Rightarrow V = \frac{{m{v_0}}}{{(m + M)}}\)(1)
Sau va chạm cơ năng của hệ được bảo toàn. Chọn W t = 0 tại vị trí cân bằng
\(\frac{1}{2}(m + M){V^2} = (m + M)gh = > \,V = \sqrt {2gh} = 0,99\,\,{\rm{m/s}}\) (Thay vào (1) ta được
\(V = \frac{{m{v_0}}}{{(m + M)}}{v_0} = \frac{{(M + m)V}}{m} = \)198,99 m/s
Sai