Đề bài
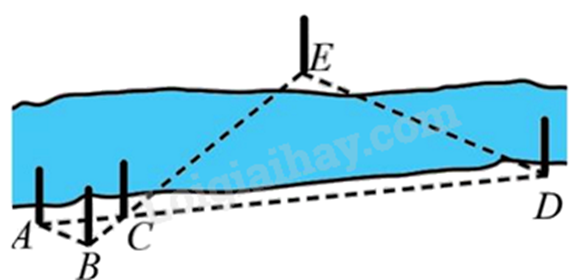
Để đo khoảng cách giữa hai địa điểm \({\rm{D}}\), \({\rm{E}}\) ở hai bên bờ của một con sông, người ta chọn các vị trí \({\rm{A}}, {\rm{B}}, {\rm{C}}\) ở cùng một bên bờ với điểm \(D\) và đo được \(AB = 2{\rm{\;m}},AC = 3{\rm{\;m}},CD = 15{\rm{\;m}}\). Giả sử $\Delta ABC\backsim \Delta DEC$. Tính khoảng cách \(DE\).
-
A.
\(10{\rm{\;m}}\)
-
B.
\(12{\rm{\;m}}\)
-
C.
\(9{\rm{\;m}}\)
-
D.
\(15{\rm{\;m}}\)
Phương pháp giải
Nếu $\Delta ABC\backsim \Delta {A}'{B}'{C}'$, ta có tỉ số các cạnh tương ứng \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{C'A'}}{{CA}} = k\) gọi là tỉ số đồng dạng.
Vì $\Delta ABC\backsim \Delta DEC$ suy ra
\(\begin{array}{l}\frac{2}{3} = \frac{{DE}}{{15}}\\DE = \frac{2}{3} \cdot 15 = 10{\rm{\;m}}\end{array}\)
Vậy \(DE = 10{\rm{\;m}}\)
Đáp án B.
Đáp án : B