Đề kiểm tra học kì 1 Toán 5 - Đề số 17
Tải vềĐáp án và lời giải chi tiết Đề số 12 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán lớp 5
Đề bài
Câu 1. Đúng ghi Đ , sai ghi S :
a) \(8{m^2}\;7d{m^2} = 870d{m^2}\)
b) \(8{m^2}\;7d{m^2} = 807d{m^2}\)
c) \(6d{m^2}\;6c{m^2} = 606c{m^2}\)
d) \(6d{m^2}\;6c{m^2} = 660c{m^2}\)
e) \(15ha\;3da{m^2} = 15\dfrac{3}{{10}}ha\)
g) \(15ha\;3da{m^2} = 15\dfrac{3}{{100}}ha\)
Câu 2. Đúng ghi Đ , sai ghi S :
Viết phân số tối giản vào chỗ chấm: \(125{m^2} = ..... ha\)
a) \(\dfrac{1}{8}\) ☐ b) \(\dfrac{1}{{80}}\) ☐ c) \(\dfrac{1}{{800}}\) ☐
Câu 3. Khoanh vào chữ đặt trước câu trả lời đúng:
Điền hỗn số vào chỗ chấm:
\(2h{m^2}345{m^2} = ...... da{m^2}\)
A. \(23\dfrac{{45}}{{100}}\) B. \(234\dfrac{5}{{100}}\)
C. \(203\dfrac{{45}}{{100}}\) D. \(230\dfrac{{45}}{{100}}\)
Câu 4. Đúng ghi Đ , sai ghi S :
Điền dấu \(\left( { > , = , < } \right)\) vào chỗ chấm:
\(2ha\;15{m^2} ..... 20015{m^2}\)
\(2\,ha15{m^2} > 20015{m^2}\) ☐
\(2\,ha15{m^2} = 20015{m^2}\) ☐
\(2\,ha15{m^2} < 20015{m^2}\) ☐
Câu 5. Khoanh vào chữ đặt trước câu trả lời đúng:
Một khu an dưỡng có diện tích là \(2\dfrac{7}{{10}}ha\), trong đó \(\dfrac{4}{9}\) là diện tích hồ nước. Hỏi diện tích còn lại là bao nhiêu mét vuông?
A. \(8000{m^2}\) B. \(10\,000{m^2}\)
C. \(12\,000{m^2}\) D. \(15\,000{m^2}\)
Câu 6. Một hình thoi có diện tích là \(\dfrac{9}{{25}}d{m^2}\). Có một đường chéo có độ dài là \(\dfrac{3}{{50}}m\). Cạnh của hình thoi bằng \(\dfrac{4}{9}\) tổng số đo hai đường chéo. Hỏi chu vi hình thoi đó là bao nhiêu xăng-ti-mét?
Câu 7. Một khu đất hình chữ nhật có chiều dài hơn chiều rộng 35m. Nếu mỗi chiều tăng thêm 5m thì diện tích tăng thêm là 1450m 2 . Hỏi khu đất đó có diện tích là bao nhiêu héc-ta?
Lời giải
Câu 1.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:
\(1m^2=100dm^2\) ; \(1dm^2= 100cm^2\) ;
\(1ha=100dam^2\) hay \(1dam^2= \dfrac{1}{100}ha\) ;
Cách giải:
+) \(8{m^2}\;7d{m^2} = 8m^2 + 7dm^2 \) \( = 800dm^2 + 7dm^2 = 807d{m^2}\) ;
+) \(6d{m^2}\;6c{m^2} = 6dm^2 + 6cm^2 \) \( = 600cm^2 + 6cm^2 = 606c{m^2}\) ;
+) \(15ha\;3da{m^2} = 15\dfrac{3}{{100}}ha\) .
Ta có kết quả như sau:
a) S; b) Đ; c) Đ;
d) S; e) S; g) Đ.
Câu 2.
Phương pháp:
Dựa vào cách chuyển đổi các đơn vị đo:
\(1ha=10\;000m^2\) hay \(1m^2= \dfrac{1}{10\;000}ha\)
Cách giải:
Ta có: \(1ha=10\;000m^2\) hay \(1m^2= \dfrac{1}{10\;000}ha\).
Do đó: \(125{m^2} =\dfrac{125}{10\;000} ha = \dfrac{1}{80}ha\).
Ta có kết quả như sau: a) S; b) Đ; c) S.
Câu 3.
Phương pháp:
Áp dụng cách chuyển đổi các đơn vị đo:
\(1hm^2=100dam^2\) ; \(1dam^2= 100m^2\) ;
Cách giải:
Ta có:
\(2h{m^2}345{m^2} = 2hm^2 + 345m^2 \) \(= 20\;000m^2 + 345m^2 = 20345{m^2}\)
Mà: \(20345{m^2} = 20300m^2 + 45m^2 \) \( = 203dam^2\; 45m^2 = 203\dfrac{{45}}{{100}}da{m^2}\)
Vậy: \(2h{m^2}345{m^2} = 203\dfrac{{45}}{{100}}da{m^2}\).
Chọn C.
Câu 4.
Phương pháp:
- Đổi các số đo về cùng đơn vị đo rồi so sánh kết quả với nhau.
- Áp dung cách đổi: \(1ha =10\;000m^2\).
Cách giải:
Ta có: \(1ha =10\;000m^2\) nên \(2ha =20\;000m^2\).
Do đó: \(2ha\;15{m^2} = 2ha+15m^2 \) \(=20\;000m^2 + 15m^2 = 20015{m^2}\)
Ta có kết quả như sau: S; Đ; S.
Câu 5.
Phương pháp:
- Đổi số đo diện tích khu an dưỡng sang đơn vị đo là mét vuông: ta có \(1ha =10\;000m^2\) nên để đổi số đo từ đơn vị \(ha\) sang đơn vị \(m^2\) ta lấy \(10\;000\) nhân với số đó.
- Tính diện tích hồ nước = diện tích khu an dưỡng \(\times \,\dfrac{4}{9}\).
- Tính diện tích còn lại = diện tích khu an dưỡng \(-\) diện tích hồ nước.
Cách giải:
Đổi: \(2\dfrac{7}{{10}}ha = \dfrac{27}{{10}}ha = 10\;000m^2 \times \dfrac{27}{{10}}\) \(=27000m^2 .\)
Diện tích hồ nước là :
\(27\;000\times \,\dfrac{4}{9} = 12\;000\;(m^2)\)
Diện tích còn lại của khu an dưỡng là:
\(27\;000- 12\;000= 15\;000\;(m^2)\)
Đáp số: \(15\,000{m^2}\).
Chọn D.
Câu 6.
Phương pháp:
- Đổi \(\dfrac{3}{{50}}m = \dfrac{3}{5}dm.\)
- Tính độ dài đường chèo còn lại ta lấy \(2\) lần diện tích chia cho độ dài đường chéo đã biết.
- Tính tổng độ dài hai đường chéo
- Tính cạnh của hình thoi = tổng độ dài hai đường chéo \(\times \dfrac{4}{9}\).
- Tính chu vi hình thoi = độ dài cạnh \(\times\;4\).
- Đổi số đo vừa tìm được sang đơn vị đo là xăng-ti-mét, lưu ý ta có: \(1dm=10cm\), hay \(1cm=\dfrac{{1}}{10}dm.\)
Cách giải:
Đổi \(\dfrac{3}{{50}}m = \dfrac{3}{5}dm.\)
Đường chéo còn lại là :
\(\dfrac{9}{{25}} \times 2:\dfrac{3}{5} = \dfrac{6}{5}\;(dm)\)
Tổng số đo hai đường chéo là:
\(\dfrac{3}{5} + \dfrac{6}{5} = \dfrac{9}{5}\;(dm)\)
Cạnh của hình thoi là:
\(\dfrac{9}{5} \times \dfrac{4}{9} = \dfrac{4}{5}\;(dm)\)
Chu vi của hình thoi là :
\(\dfrac{4}{5} \times 4 = \dfrac{{16}}{5}\;(dm)\)
\(\dfrac{{16}}{5}dm = \dfrac{{32}}{10}dm= 32cm\)
Đáp số: \(32cm.\)
Câu 7.
Phương pháp:
- Vẽ hình dựa vào dữ kiện đề bài (xem hình trong phần lời giải).
- Chia phần tăng thêm thành các hình chữ nhật nhỏ, dựa vào diện tích và độ dài cạnh đã biết để tính độ dài còn lại.
- Áp dụng các công thức:
Diện tích = chiều dài \(\times\) chiều rộng;
Chiều dài = diện tích : chiều rộng ;
Chiều rộng = diện tích : chiều dài.
Cách giải:
Theo đề bài ta có hình vẽ:
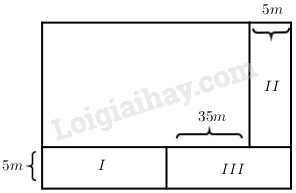
Chia phần tăng thêm thành ba hình chữ nhật như hình vẽ.
Hình III có chiều rộng là \(5m\), chiều dài là \(35 + 5 = 40 \;(m)\).
Diện tích hình III là:
\(40 \times 5 = 200\;({m^2})\)
Hình I bằng hình II vì đều có chiều rộng bằng \(5m\) và chiều dài bằng chiều rộng cũ của khu đất.
Tổng diện tích khu đất hình I và hình II là:
\(1450 - 200= 1250\;({m^2})\)
Diện tích hình I hay hình II là :
\(1250 :2 = 625\;({m^2})\)
Chiều rộng của khu đất là :
\(625:5 = 125\;(m)\)
Chiều dài của khu đất là :
\(125 + 35 = 160\;(m)\)
Diện tích của khu đất là :
\(160 \times 125 = 20\;000\;({m^2})\)
\(20\;000{m^2} = 2ha\)
Đáp số: \(2ha\).