Đề thi học kì 1 Toán 6 - Đề số 10 - Chân trời sáng tạo
Tải vềPhần I: Trắc nghiệm (5 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
Phần I: Trắc nghiệm (5 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Chu vi của hình lục giác đều cạnh bằng 3cm là:
A. 9 cm B. 12 cm C. 18 cm D. 24 cm
Câu 2: Số đối của số -5 là:
A. -5 B. \(\dfrac{1}{5}\) C. 5 D. 0
Câu 3: Bạn Lan mua 5 quyển vở và 2 chiếc bút. Biết một chiếc bút giá 3500 đồng, một quyển vở giá 12000 đồng. Hỏi bạn Lan mua hết bao nhiêu tiền?
A. 24000 đồng B. 67000 đồng C. 130000 đồng D. 41500 đồng
Câu 4: Cho tập hợp \(A = \left\{ {1;a;2;5;b} \right\}\). Trong các khẳng định sau khẳng định nào sai ?
A. \(1 \in A\) B. \(25 \in A\) C. \(0 \notin A\) D. \(b \in A\)
Câu 5: Tập hợp B gồm các số tự nhiên lớn hơn 3 và nhỏ hơn 6 được viết là:
A. \(B = \left[ {4;5} \right]\) B. \(B = \left\{ {4;5} \right\}\) C. \(B = \left( {4;5} \right)\) D. \(B = \left\{ {3;4;5;6} \right\}\)
Câu 6: Sắp xếp các số nguyên sau theo thứ tự tăng dần: \( - 3;1;0; - 5\).
A. \( - 5; - 3;0;1\) B. \(0;1; - 3; - 5\) C. \(1;0; - 3; - 5\) D. \( - 5; - 3;1;0\)
Câu 7: Nhiệt độ lúc 12 giờ ở đỉnh mẫu Sơn (thuộc tỉnh Lạng Sơn) vào một ngày mùa đông là \({1^0}C\), đến 17 giờ nhiệt độ giảm thêm \({3^0}C\). Nếu đến 23 giờ cùng ngày nhiệt độ giảm thêm \({2^0}C\) nữa thì nhiệt độ lúc 23 giờ là:
A. \({5^0}C\) B. \( - {5^0}C\) C. \({0^0}C\) D. \( - {4^0}C\)
Câu 8: Biểu đồ tranh dưới đây biểu diễn số lượng đôi giày thể thao bán được của một của hàng trong 4 năm gần đây:
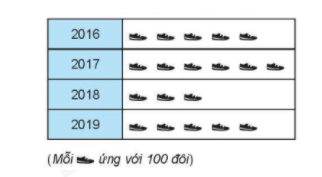
Hãy tính tổng số lượng đôi giày thể thao bán được của năm 2017 và năm 2019?
A. \(1000\) đôi giày B. \(1100\) đôi giày C. \(1010\) đôi giày D. \(11000\) đôi giày
Câu 9: Cho số tự nhiên x thỏa mãn \(21 - x = 3\). Số liền sau của x là:
A. 18 B. 19 C. 25 D. 24
Câu 10: Trong các hình sau, hình nào là tam giác đều?
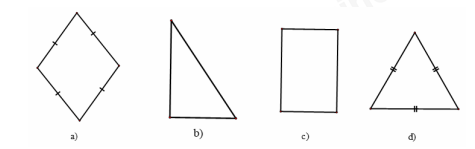
A. b. B. a. C. c. D. d.
Câu 11: Kết quả của phép tính \({5^{15}}{.5^5}\) là:
A. \({25^{75}}\) B. \({5^{75}}\) C. \({10^{20}}\) D. \({5^{20}}\)
Câu 12: Một hình thoi có độ dài hai đường chéo là 6cm và 8cm. Diện tích hình thoi đó là:
A. \(24\,\,c{m^2}\) B. \(48\,\,c{m^2}\) C. \(14\,\,c{m^2}\) D. \(28\,\,c{m^2}\)
Câu 13: Phát biểu nào sau đây là đúng?
A. Bảng thống kê là một cách trình bày dữ liệu chi tiết hơn bảng dữ liệu ban đầu, bao gồm các hàng và các cột, thể hiện danh sách các đối tượng thống kê cùng với các dữ liệu của đối tượng đó.
B. Bảng thống kê là một cách trình bày dữ liệu tóm tắt hơn bảng dữ liệu ban đầu, bao gồm các hàng và các cột, thể hiện danh sách các đối tượng thống kê cùng với các dữ liệu của đối tượng đó.
C. Cả A, B đều đúng.
D. Cả A, B đều sai.
Câu 14: Trong các số sau số nào chia hết cho cả 2, 5 và 9?
A. 960 B. 2580 C. 5430 D. 17910
Câu 15: Có bao nhiêu số nguyên x thỏa mãn \( - 2 < x \le 1\)?
A. 1 B. 2 C. 3 D. 4
Câu 16: Trong các số 1; 2; 4; 5; 9 thì các số nguyên tố là
A. 5; 9 B. 2; 5 C. 1; 2; 5 D. 2; 5; 9
Câu 17: Hình nào sau đây luôn có tất cả các cạnh bằng nhau?
A. Hình thang B. Hình bình hành C. Hình thoi D. Hình chữ nhật
Câu 18: Cho \(A = 1 - 2 + 3 - 4 + 5 - 6 + ... + 47 - 48 + 49 - 50\). Tính A.
A. A = -25 B. A = 25 C. A = -50 D. A = 0
Câu 19: Số La Mã XXI biểu diễn số tự nhiên
A. 21 B. 19 C. 20 D. 111
Câu 20: Số nguyên x thỏa mãn \(x + 5 = - 2\) là:
A. 21 B. 19 C. 20 D. 111
PHẦN II. PHẦN CÂU HỎI TỰ LUẬN (5,0 điểm)
Câu 1: (2,0 điểm)
1) Thực hiện phép tính: \(5.\left( {{2^3} + 1} \right) - 9\).
2) Một chiếc tàu ngầm đang thám hiểm đại dương ở độ cao -123m so với mực nước biển. Sau khi hoàn thiện nhiệm vụ, tàu nổi cao lên thêm 82m. Tính độ cao mới của tầm ngầm so với mực nước biển.
Câu 2: (1,0 điểm)
Để khen thưởng học sinh của lớp có thành tích trong học kì I, giáo viên chủ nhiệm cùng phụ huynh học sinh đã chuẩn bị 120 quyển vở và 72 chiếc bút. Số vở và số bút được chia đều cho các phần thưởng. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng.
Câu 3: (1,5 điểm)
1. Vẽ hình vuông có cạnh bằng 3cm.
2. Một sân bóng mini hình chữ nhật có chiều dài 30m và chiều rộng 20m.
a) Tính diện tích của sân bóng mini đó.
b) Với tổng số tiền mua cỏ nhân tạo là 27 000 000 đồng thì vừa đủ để trái kín mặt sân. Hỏi giá tiền mỗi mét vuông cỏ nhân tạo đó là bao nhiêu?
Câu 4: (0,5 điểm)
Cho \(A = 1 + 2 + {2^2} + ... + {2^{2020}} + {2^{2021}}\) và \(B = {2^{2022}}\). Chứng minh A và B là hai số tự nhiên liên tiếp.
Lời giải
I. PHẦN TRẮC NGHIỆM (5,0 điểm)
|
1. C |
2. C |
3. B |
4. B |
5. B |
6. A |
7. D |
8. B |
9. B |
10. D |
|
11. D |
12. A |
13. A |
14. D |
15. C |
16. B |
17. C |
18. A |
19. A |
20. D |
Câu 1
Phương pháp:
Lục giác đều có 6 cạnh bằng nhau.
Chu vi của hình lục giác là tổng độ dài 6 cạnh.
Cách giải:
Chu vi của hình lục giác đều cạnh bằng 3cm là 6.3 = 18 (cm).
Chọn C.
Câu 2
Phương pháp:
Số đối của a là –a. Số đối của 0 là chính nó.
Cách giải:
Số đối của số -5 là 5.
Chọn C.
Câu 3
Phương pháp:
- Tính số tiền mua 5 quyển vở.
- Tính số tiền mua 2 chiếc bút.
- Tính tổng số tiền.
Cách giải:
Số tiền để mua 5 quyển vở là:
\(5.12000 = 60000\) (đồng)
Số tiền để mua 2 chiếc bút là:
\(2.3500 = 7000\) (đồng)
Tổng số tiền để mua 5 quyển vở và 2 chiếc bút là:
\(60000 + 7000 = 67000\) (đồng)
Chọn B.
Câu 4
Phương pháp:
Xác định phần tử thuộc A và không thuộc A.
Cách giải:
\(1 \in A,\,\,25 \notin A,\,\,0 \notin A,\,\,b \in A\) nên đáp án B sai.
Chọn B.
Câu 5
Phương pháp:
Mô tả tập hợp theo cách liệt kê các phần tử của tập hợp, tức là viết các phần tử của tập hợp trong dấu { } theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.
Cách giải:
\(B = \left\{ {4;5} \right\}\).
Chọn B.
Câu 6
Phương pháp:
Sắp xếp các số nguyên sau theo thứ tự tăng dần, tức là sắp xếp theo thứ tự từ nhỏ đến lớn theo chiều từ trái qua phải.
Cách giải:
Sắp xếp các số nguyên sau theo thứ tự tăng dần: \( - 3;1;0; - 5\) ta được \( - 5; - 3;0;1\).
Chọn A.
Câu 7
Phương pháp:
- Tính nhiệt độ lúc 17 giờ.
- Tính nhiệt độ lúc 23 giờ.
- Sử dụng quy tắc cộng trừ hai số nguyên.
Cách giải:
Nhiệt độ lúc 17 giờ là: \(1 - 3 = - 2\,\,\left( {^0C} \right)\)
Nhiệt độ lúc 23 giờ là: \( - 2 - 2 = - 4\,\,\left( {^0C} \right)\).
Chọn D.
Câu 8
Phương pháp:
Đọc dữ liệu ở biểu đồ tranh, thực hiện phép tính nhân
Cách giải:
Vì tổng số hình
 của năm 2017 và năm 2019 là \(11\) hình nên tổng số lượng đôi giày thể thao bán được của năm 2017 và năm 2019 là: \(11.100 = 1100\) (đôi giày)
của năm 2017 và năm 2019 là \(11\) hình nên tổng số lượng đôi giày thể thao bán được của năm 2017 và năm 2019 là: \(11.100 = 1100\) (đôi giày)
Chọn B.
Câu 9
Phương pháp:
- Tìm x.
- Tìm số liền sau của x (là số lớn hơn x 1 đơn vị).
Cách giải:
\(\begin{array}{l}21 - x = 3\\\,\,\,\,\,\,\,\,\,\,x = 21 - 3\\\,\,\,\,\,\,\,\,\,\,x = 18\end{array}\)
Vậy số liền sau của x là 19.
Chọn B.
Câu 10
Phương pháp:
Nhận biết tam giác đều: là tam giác có 3 cạnh bằng nhau.
Cách giải:
Tam giác đều là hình d.
Chọn D.
Câu 11
Phương pháp:
Sử dụng công thức: \({a^m}.{a^n} = {a^{m + n}}\).
Cách giải:
\({5^{15}}{.5^5} = {5^{15 + 5}} = {5^{20}}\)
Chọn D.
Câu 12
Phương pháp:
Diện tích hình thoi bằng nửa tích hai đường chéo.
Cách giải:
Diện tích hình thoi là: \(\dfrac{1}{2}.6.8 = 24\,\,\left( {c{m^2}} \right)\).
Chọn A.
Câu 13
Phương pháp:
Sử dụng lý thuyết bảng thống kê.
Cách giải:
Bảng thống kê là một cách trình bày dữ liệu chi tiết hơn bảng dữ liệu ban đầu, bao gồm các hàng và các cột, thể hiện danh sách các đối tượng thống kê cùng với các dữ liệu của đối tượng đó.
Chọn A.
Câu 14
Phương pháp:
Sử dụng dấu hiệu chia hết cho 2 và 5: là số có tận cùng bằng 0.
Sử dụng dấu hiệu chia hết cho 9: có tổng các chữ số chia hết cho 9.
Cách giải:
Số chia hết cho 2 và 5 là số có tận cùng là 0.
Số chia hết cho 9 là số có tổng các chữ số chia hết cho 9.
Nên loại đáp án A, B, C.
Chọn D.
Câu 15
Phương pháp:
Liệt kê các số x thỏa mãn và đếm.
Cách giải:
\( - 2 < x \le 1\) thì \(x \in \left\{ { - 1;0;1} \right\}\) nên có 3 số nguyên x thỏa mãn.
Chọn C.
Câu 16
Phương pháp:
Số nguyên tố là các số chỉ chia hết cho 1 và chính nó.
Số 1 không là số nguyên tố.
Cách giải:
Trong các số 1; 2; 4; 5; 9 thì các số nguyên tố là 2; 5.
Chọn B.
Câu 17
Phương pháp:
Nhận biết các hình.
Cách giải:
Hình có tất cả các cạnh bằng nhau là hình thoi.
Chọn C.
Câu 18
Phương pháp:
Sử dụng quy tắc kết hợp phù hợp.
Cách giải:
\(\begin{array}{l}A = 1 - 2 + 3 - 4 + 5 - 6 + ... + 47 - 48 + 49 - 50\\A = \left( {1 - 2} \right) + \left( {3 - 4} \right) + \left( {5 - 6} \right) + ... + \left( {47 - 48} \right) + \left( {49 - 50} \right)\\A = \left( { - 1} \right) + \left( { - 1} \right) + \left( { - 1} \right) + ... + \left( { - 1} \right) + \left( { - 1} \right)\\A = \left( { - 1} \right).25\\A = - 25\end{array}\)
Chọn A.
Câu 19
Phương pháp
Sử dụng cách viết số La Mã và các quy tắc viết số La Mã.
Cách giải:
Số La Mã XXI biểu diễn số tự nhiên 21.
Chọn A.
Câu 20
Phương pháp:
Giải bài toán tìm x.
Cách giải:
\(\begin{array}{l}x + 5 = - 2\\x\,\,\,\,\,\,\,\,\, = - 2 - 5\\x\,\,\,\,\,\,\,\,\, = - 7\end{array}\)
Chọn D.
PHẦN II. PHẦN CÂU HỎI TỰ LUẬN (5,0 điểm)
Câu 1:
Phương pháp:
1) Thực hiện phép tính theo thứ tự trong ngoặc trước, ngoài ngoặc sau, nếu chỉ có phép cộng và trừ thực hiện theo thứ tự từ trái qua phải hoặc nhóm số hạng phù hợp.
2) Sử dụng quy tắc cộng hai số nguyên khác dấu.
Cách giải:
1)
\(\begin{array}{l}\,\,\,\,5.\left( {{2^3} + 1} \right) - 9\\ = 5.\left( {8 + 1} \right) - 9\\ = 5.9 - 9\\ = 45 - 9\\ = 46\end{array}\)
2) Độ cao mới của tàu ngầm so với mục nước biển là:
\( - 123 + 82 = - 41\,\,\left( m \right)\)
Đáp số: -41m.
Câu 2:
Phương pháp:
Số phần thưởng được chia nhiều nhất là ƯCLN(120;72).
Cách giải:
Số phần thưởng được chia nhiều nhất là ƯCLN(120;72).
Ta có:
\(\begin{array}{l}120 = {2^3}.3.5\\72 = {2^3}{.3^2}\end{array}\)
\( \Rightarrow \) ƯCLN(120,72) = \({2^3}.3 = 24\).
Vậy có thể chia được nhiều nhất 24 phần thưởng.
Câu 3
Phương pháp:
1. Vẽ tứ giác có 4 cạnh bằng 3cm.
2.
a) Diện tích hình chữ nhật bằng tích chiều dài và chiều rộng.
b) Tính số tiền mỗi mét vuông bằng tổng số tiền chia diện tích.
Cách giải:
a) Vẽ hình vuông cạnh 3cm.
2.
a) Diện tích của sân bóng mini đó là:
30.20 = 600 \(\left( {{m^2}} \right)\).
b) Giá tiền mỗi mét vuông cỏ nhân tạo đó là:
\(27\,000\,000:600 = 45\,000\) (đồng).
Câu 4
Phương pháp
Tính 2A và sử dụng phép trừ 2A – A, từ đó tính A.
Cách giải:
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,A = 1 + 2 + {2^2} + ... + {2^{2020}} + {2^{2021}}\\ \Rightarrow 2A = 2 + {2^2} + {2^3} + ... + {2^{2021}} + {2^{2022}}\\ \Rightarrow 2A - A = {2^{2022}} - 1\\ \Rightarrow A = {2^{2022}} - 1\end{array}\)
Vậy A và B là hai số tự nhiên liên tiếp.