Đề thi học kì 2 môn toán lớp 9 năm 2019 - 2020 trường THCS Hoàng Văn Thụ — Không quảng cáo

Đề bài

Câu 1 (2 điểm):

Cho hàm số \(\left( P \right):y = {x^2}\) và hàm số \(\left( D \right):y =  - x + 6\)

a) Vẽ \(\left( P \right)\) và \(\left( D \right)\) trên cùng một hệ trục tọa độ.

b) Tìm các tọa độ giao điểm của \(\left( P \right)\) và \(\left( D \right)\) bằng phép tính.

Câu 2 (2 điểm):

Giải phương trình và hệ phương trình

a) \(3{x^2} + 4\left( {x - 2} \right) = 7\)

b) \(\left\{ \begin{array}{l} - 3\left( {x + 1} \right) - y = 5\\4x - 5\left( {y - 2} \right) = 12\end{array} \right.\)

Câu 3 (1 điểm):

Cho phương trình \({x^2} - \left( {m - 3} \right)x + m - 4 = 0\)

a) Chứng minh phương trình luôn có nghiệm với mọi \(m\).

b) Tìm \(m\) để phương trình có 2 nghiệm thỏa: \(x_1^2 + x_2^2 + 5{x_1} + 5{x_2} = 30\).

Câu 4 (1 điểm):

Một miếng đất hình chữ nhật có chu vi là \(120\,m\) và chiều dài gấp \(3\) lần chiều rộng. Tính kích thước miếng đất?

Câu 5 (1 điểm):

Máy kéo nông nghiệp có bánh xe sau to hơn bánh xe trước. Bánh xe sau có đường kính là \(1,672\,m\) và bánh xe trước có đường kính là \(88\,cm\). Hỏi khi xe chạy trên đoạn đường thẳng, bánh xe sau lăn được \(10\) vòng thì xe di chuyển được bao nhiêu mét và khi đó bánh xe trước lăn được mấy vòng?

Câu 6 (3 điểm):

Cho tam giác \(ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right)\). Các đường cao \(AD\), \(BE,CF\) của \(\Delta ABC\) cắt nhau tại \(H\).

a) Chứng minh các tứ giác \(AFHE,BFEC\) nội tiếp đường tròn.

b) Chứng minh \(AB.CE = HC.BE\).

c) Chứng minh \(H\) là tâm đường tròn nội tiếp \(\Delta DEF\).

HẾT

LG câu 1

Phương pháp giải:

a) Lập bảng giá trị rồi vẽ đồ thị hàm số

b) Giải phương trình hoành độ giao điểm, sau đó thay hoành độ tìm được vào các hàm số để tìm tung độ giao điểm.

Lời giải chi tiết:

Cho hàm số \(\left( P \right):y = {x^2}\) và hàm số \(\left( D \right):y =  - x + 6\)

a) Vẽ \(\left( P \right)\) và \(\left( D \right)\) trên cùng một hệ trục tọa độ.

Vẽ \(\left( P \right):y = {x^2}\)

Bảng giá trị:

Vẽ parabol đi qua các điểm có tọa độ \(\left( { - 2;4} \right),\left( { - 1;1} \right),\left( {0;0} \right),\) \(\left( {1;1} \right),\left( {2;4} \right)\) ta được đồ thị hàm số \(\left( P \right):y = {x^2}\)

Vẽ  \(\left( D \right):y =  - x + 6\)

Với \(x = 2 \Rightarrow y = 4\). Điểm \(\left( {2;4} \right)\) thuộc \(\left( D \right)\)

Với \(x = 0 \Rightarrow y = 6\). Điểm \(\left( {0;6} \right)\) thuộc \(\left( D \right)\)

Vẽ đường thẳng đi qua hai điểm \(\left( {2;4} \right)\) và \(\left( {0;6} \right)\) ta được đường thẳng \(\left( D \right):y =  - x + 6\)

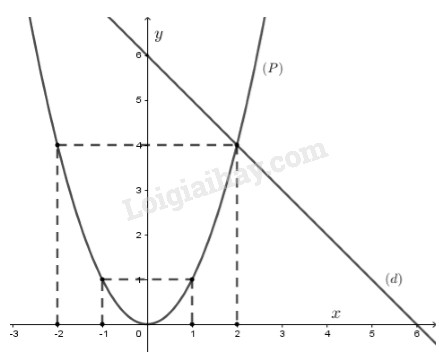
b) Tìm các tọa độ giao điểm của \(\left( P \right)\) và \(\left( D \right)\) bằng phép tính.

Xé phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( D \right)\), ta có:

\({x^2} =  - x + 6\)

\(\begin{array}{l} \Leftrightarrow {x^2} + x - 6 = 0\\ \Leftrightarrow {x^2} + 3x - 2x - 6 = 0\\ \Leftrightarrow x\left( {x + 3} \right) - 2\left( {x + 3} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x + 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x =  - 3\end{array} \right.\end{array}\)

Với \(x = 2\)\( \Rightarrow y = {x^2} = {2^2} = 4\)

Với \(x =  - 3\) \( \Rightarrow y = {x^2} = {\left( { - 3} \right)^2} = 9\)

Tọa độ giao điểm của \(\left( P \right)\) và \(\left( D \right)\) là \(\left( {2;4} \right),\left( { - 3;9} \right)\).

LG câu 2

Phương pháp giải:

a) Phá ngoặc sau đó sử dụng công thức nghiệm của phương trình bậc hai

b) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số

Lời giải chi tiết:

a) \(3{x^2} + 4\left( {x - 2} \right) = 7\)

\(\begin{array}{l} \Leftrightarrow 3{x^2} + 4x - 8 - 7 = 0\\ \Leftrightarrow 3{x^2} + 4x - 15 = 0\end{array}\)

Ta có: \(\Delta ' = {2^2} - 3.\left( { - 15} \right)\)\( = 49 > 0\)

Nên phương trình có hai nghiệm:

\(\left[ \begin{array}{l}x = \dfrac{{ - 2 + \sqrt {49} }}{3}\\x = \dfrac{{ - 2 - \sqrt {49} }}{3}\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{5}{3}\\x =  - 3\end{array} \right.\)

Vậy nghiệm của phương trình đã cho là \(x =  - 3;x = \dfrac{5}{3}.\)

b) \(\left\{ \begin{array}{l} - 3\left( {x + 1} \right) - y = 5\\4x - 5\left( {y - 2} \right) = 12\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} - 3x - 3 - y - 5 = 0\\4x - 5y + 10 - 12 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 3x - y - 8 = 0\\4x - 5y - 2 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 15x - 5y - 40 = 0\\4x - 5y - 2 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}19x + 38 = 0\\4x - 5y - 2 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}19x =  - 38\\4x - 5y - 2 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 2\\4.\left( { - 2} \right) - 5y - 2 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 2\\ - 5y - 10 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 2\\ - 5y = 10\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 2\\y =  - 2\end{array} \right.\end{array}\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( { - 2; - 2} \right)\)

LG câu 3

Phương pháp giải:

a) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có nghiệm \( \Leftrightarrow \Delta  \ge 0\)

b) Sử dụng hệ thức Vi-et: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)

Lời giải chi tiết:

Cho phương trình \({x^2} - \left( {m - 3} \right)x + m - 4 = 0\)

a) Chứng minh phương trình luôn có nghiệm với mọi \(m\) .

Phương trình \({x^2} - \left( {m - 3} \right)x + m - 4 = 0\) (*) có hệ số \(a = 1 \ne 0\) nên là phương trình bậc hai một ẩn.

Ta có: \(\Delta  = {\left( {m - 3} \right)^2} - 4.1.\left( {m - 4} \right)\) \( = {m^2} - 6m + 9 - 4m + 16\) \( = {m^2} - 10m + 25\) \( = {\left( {m - 5} \right)^2}\)

Vì \(\Delta  = {\left( {m - 5} \right)^2} \ge 0\) với mọi \(m\) nên phương trình (*) luôn có nghiệm với mọi \(m.\)

b) Tìm \(m\) để phương trình có 2 nghiệm thỏa: \(x_1^2 + x_2^2 + 5{x_1} + 5{x_2} = 30\) .

Vì phương trình (*) luôn có nghiệm với mọi \(m\) (theo câu a) nên gọi \({x_1};{x_2}\) là hai nghiệm của phương trình, theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m - 3\\{x_1}{x_2} = m - 4\end{array} \right.\)

Xét  \(x_1^2 + x_2^2 + 5{x_1} + 5{x_2} = 30\)

\( \Leftrightarrow x_1^2 + x_2^2 + 2{x_1}{x_2} - 2{x_1}{x_2}\) \( + 5{x_1} + 5{x_2} = 30\)

\( \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\) \( + 5\left( {{x_1} + {x_2}} \right) = 30\)

\( \Leftrightarrow {\left( {m - 3} \right)^2} - 2\left( {m - 4} \right)\) \( + 5\left( {m - 3} \right) = 30\)

\( \Leftrightarrow {m^2} - 6m + 9 - 2m + 8\) \( + 5m - 15 - 30 = 0\)

\( \Leftrightarrow {m^2} - 3m - 28 = 0\)

\(\begin{array}{l} \Leftrightarrow {m^2} - 7m + 4m - 28 = 0\\ \Leftrightarrow m\left( {m - 7} \right) + 4\left( {m - 7} \right) = 0\\ \Leftrightarrow \left( {m - 7} \right)\left( {m + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 7 = 0\\m + 4 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = 7\\m =  - 4\end{array} \right.\end{array}\)

Vậy \(m = 7;m =  - 4\) thỏa mãn yêu cầu đề bài.

LG câu 4

Phương pháp giải:

Giải bài toán bằng cách lập phương trình

B1: Chọn ẩn và đặt điểu kiện cho ẩn

B2: Lập phương trình và giải phương trình

B3: Kết hợp điều kiện và kết luận

Lời giải chi tiết:

Gọi chiều rộng của hình chữ nhật là \(x\left( {x > 0} \right)\) (m)

Vì chiều dài gấp \(3\) lần chiều rộng nên chiều dài là \(3x\) (m)

Chu vi hình chữ nhật là \(120m\) nên ta có phương trình:

\(\left( {x + 3x} \right).2 = 120\)

\(\begin{array}{l} \Leftrightarrow 4x.2 = 120\\ \Leftrightarrow 8x = 120\end{array}\)

\( \Leftrightarrow x = 15\) (thỏa mãn)

Vậy chiều rộng của hình chữ nhật là \(15m\) và chiều dài hình chữ nhật là \(15.3 = 45m\).

LG câu 5

Phương pháp giải:

- Tính chu vi mỗi bánh xe.

- Tính quãng đường bánh xe sau lăn được \(10\) vòng, từ đó suy ra quãng đường xe đi được và cũng là quãng đường bánh xe trước lăn được.

- Tính số vòng quay bánh xe trước lăn được.

Chú ý công thức:

Quãng đường \( = \) chu vi \( \times \) số vòng quay

Lời giải chi tiết:

Máy kéo nông nghiệp có bánh xe sau to hơn bánh xe trước. Bánh xe sau có đường kính là \(1,672\,m\) và bánh xe trước có đường kính là \(88\,cm\) . Hỏi khi xe chạy trên đoạn đường thẳng, bánh xe sau lăn được \(10\) vòng thì xe di chuyển được bao nhiêu mét và khi đó bánh xe trước lăn được mấy vòng?

Đổi \(1,672\,m = 167,2\,cm\).

Chu vi bánh xe sau là: \({C_s} = \pi .167,2 = 167,2\pi \,\,\left( {cm} \right)\)

Chu vi bánh xe trước là: \({C_t} = \pi .88 = 88\pi \,\,\left( {cm} \right)\)

Khi bánh xe sau lăn được \(10\) vòng thì xe di chuyển được quãng đường là:

\(10.167,2\pi  = 1672\pi \left( {cm} \right)\) \( \approx 5253\left( {cm} \right) = 52,53\left( m \right)\)

Bánh xe trước lăn được số vòng là:

\(1672\pi :88\pi  = 19\) (vòng)

Vậy xe đi được quãng đường \(52,53m\) và bánh trước lăn được \(19\) vòng.

LG câu 6

Phương pháp giải:

a) Chứng minh hai tứ giác có tổng một cặp góc đối bằng \({180^0}\).

b) Chứng minh \(\Delta ABE\) đồng dạng \(\Delta HCE\) theo trường hợp góc – góc.

c) Chứng minh \(EH,FH\) lần lượt là các tia phân giác của \(\widehat E,\widehat F\).

Lời giải chi tiết:

Cho tam giác \(ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right)\) . Các đường cao \(AD\) , \(BE,CF\) của \(\Delta ABC\) cắt nhau tại \(H\) .

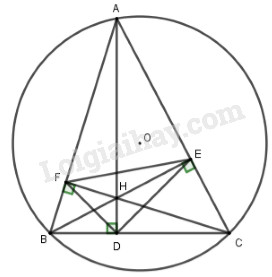
a) Chứng minh các tứ giác \(AFHE,BFEC\) nội tiếp đường tròn.

Ta có: \(BE \bot AC\) \( \Rightarrow \widehat {AEH} = {90^0}\)

\(CF \bot AB\) \( \Rightarrow \widehat {AFH} = {90^0}\)

Xét tứ giác \(AFHE\) có:

\(\widehat {AFH} + \widehat {AEH} = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\))

Xét tứ giác \(BFEC\) có:

\(\widehat { BFC } = \widehat {BEC} = {90^0}\) nên là tứ giác nội tiếp (tứ giác có hai đỉnh cùng nhìn một cạnh các góc bằng nhau).

Vậy các tứ giác \(AFHE,BFEC\) nội tiếp đường tròn. (đpcm)

b) Chứng minh \(AB.CE = HC.BE\) .

Theo câu a, tứ giác \(BFEC\) nội tiếp nên \(\widehat {FBE} = \widehat {FCE}\) (góc nội tiếp cùng chắn cung \(EF\))

\( \Rightarrow \widehat {ABE} = \widehat {HCE}\).

Xét \(\Delta ABE\) và \(\Delta HCE\) có:

\(\begin{array}{l}\widehat {ABE} = \widehat {HCE}\left( {cmt} \right)\\\widehat {AEB} = \widehat {HEC} = {90^0}\\ \Rightarrow \Delta ABE \backsim \Delta HCE\left( {g - g} \right)\end{array}\)

\( \Rightarrow \dfrac{{AB}}{{HC}} = \dfrac{{BE}}{{CE}}\) (cạnh tương ứng)

\( \Rightarrow AB.CE = HC.BE\) (đpcm).

c) Chứng minh \(H\) là tâm đường tròn nội tiếp \(\Delta DEF\) .

Xét tứ giác \(EHDC\) có: \(\widehat {HEC} + \widehat {HDC} = {90^0} + {90^0} = {180^0}\)

Do đó \(EHDC\) nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\))

\( \Rightarrow \widehat {HED} = \widehat {HCD}\) (góc nội tiếp cùng chắn cung \(HD\))

\( \Rightarrow \widehat {BED} = \widehat {FCB}\) (1)

Lại có, tứ giác \(BFEC\) nội tiếp nên \(\widehat {FEB} = \widehat {FCB}\) (góc nội tiếp cùng chắn cung \(FB\)) (2)

Từ (1) và (2) suy ra \(\widehat {BED} = \widehat {FEB}\left( { = \widehat {FCB}} \right)\) hay \(EB\) là tia phân giác của \(\widehat {FED}\).

Xét tứ giác \(BFHD\) có \(\widehat {BFH} + \widehat {BDH} = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\))

\( \Rightarrow \widehat {HFD} = \widehat {HBD}\) (góc nội tiếp cùng chắn cung \(HD\))

\( \Rightarrow \widehat {CFD} = \widehat {EBC}\) (3)

Tứ giác \(BFEC\) nội tiếp (câu a) \( \Rightarrow \widehat {EBC} = \widehat {EFC}\) (góc nội tiếp cùng chắn cung \(EC\)) (4)

Từ (3) và (4) suy ra \(\widehat {EFC} = \widehat {CFD}\left( { = \widehat {EBC}} \right)\) hay \(FC\) là tia phân giác của \(\widehat {EFD}\).

Tam giác \(DEF\) có hai đường phân giác các góc \(\widehat E,\widehat F\) cắt nhau tại \(H\) nên \(H\) là tâm đường tròn nội tiếp tam giác \(DEF\) (đpcm).

HẾT