Đề thi học kì 2 Toán 7 - Đề số 10 — Không quảng cáo

Đề bài

I. TRẮC NGHIỆM (2 điểm)

Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1: Bậc của đa thức \( - {x^8} - {x^2} + {x^9} + {x^5} - 12{x^3} - {x^9} + 10\) là

A. 10 B. \(8\) C. \(9\) D. \(7\)

Câu 2: Hình hộp chữ nhật có bao nhiêu cạnh?

A. 12. B. 8. C. 16. D. 6.

Câu 3: Đội múa có 1 bạn nữ và 5 bạn nam. Chọn ngẫu nhiên 1 bạn để phỏng vấn. Biết mỗi bạn đều có khả năng được chọn. Tính xác suất của biến cố “Bạn được chọn là nữ”.

A. 1. B. \(\dfrac{1}{5}\). C. \(\dfrac{5}{6}\). D. \(\dfrac{1}{6}\).

Câu 4: Cho \(\Delta ABC\) có AD  là tia phân giác, \(\hat B = {40^\circ },\hat C = {60^\circ }\). Khi đó số đo của \(\widehat {BAD}\) là :

A. \({40^\circ }\). B. \({60^\circ }\). C. \({70^\circ }\). D. \({100^\circ }\).

Câu 5: Tam giác DEF có số đo các cạnh là \(DE = 5cm\); \(DF = 7cm\) và \(EF = 8cm\). So sánh các góc của tam giác DEF ta có:

A. \(\angle D > \angle E > \angle F\). B. \(\angle D < \angle E < \angle F\). C. \(\angle E > \angle D > \angle F\). D. \(\angle D > \angle F > \angle E\).

Câu 6: Trong các giá trị sau đây, đâu là nghiệm của đa thức 5x ² − 3x – 2?

A. x = 1 B. x =  - 1 C. \(x = \dfrac{2}{5}\) D. \(x = {\rm{ \;}} - \dfrac{2}{5}\)

Câu 7: Thu gọn biểu thức \(\left( {x - 2} \right)\left( {3x + 1} \right) - \left( { - 3x + 2} \right)\left( {1 - x} \right)\) ta được:

A. \(1\) B. \( - 4\) C. \(2\) D. \(0\)

Câu 8: Cho tam giác MNP cân tại \(M\) có \(\angle N = {50^0}\). Số đo của góc \(M\) là:

A. \({65^0}\) B. \({50^0}\) C. \({130^0}\) D. \({80^0}\)

II. TỰ LUẬN

Câu 1:

Hưởng ứng phong trào: “Phát triển văn hóa đọc trong kỷ nguyên số”, ba lớp 7A, 7B, 7C đóng góp cho thư viện nhà trường được 300 quyển sách. Biết rằng số sách đóng góp cho thư viện của ba lớp 7A, 7B, 7C tỉ lệ với 5; 3; 7. Tính số sách đóng góp cho thư viện của mỗi lớp.

Câu 2:

Cho hai đa thức:

\(A\left( x \right) = 9 - {x^5} + 2{x^3} - 10{x^4} + 3{x^2} + 3{x^4} - 2{x^2} - 4x\);

\(B\left( x \right) = {x^5} - 9 + 7{x^4} - 3x - {x^2} + 5{x^3} + 6x - 3{x^3}\).

a) Thu gọn và sắp xếp các đa thức theo lũy thừa giảm của biến.

b) Tính \(A\left( x \right) + B\left( x \right);{\mkern 1mu} A\left( x \right) - B\left( x \right)\).

c) Tìm nghiệm của đa thức \(H\left( x \right) = A\left( x \right) + B\left( x \right)\).

Câu 3: Cho \(\Delta ABC\) vuông tại \(B\) , đường cao \(BK\left( {K \in AC} \right).\) Vẽ BH là tia phân giác của \(\angle ABK\left( {H \in AC} \right).\) Kẻ HD vuông góc với AB.

a) Chứng minh \(\Delta\)BHK = \(\Delta\)BHD

b) Gọi giao điểm của DH và BK là \(I\). Chứng minh : \(IK = AD.\)

c) Chứng minh \(DK//AI\)

d) Các đường phân giác của \(\Delta BKC\) cắt nhau tại \(M\) . Gọi \({\rm{N}}\) là giao điểm của \(CM{\mkern 1mu} \)và BK. Chứng minh \({\rm{N}}\) là trực tâm của \(\Delta BHC.\)

Câu 4: Tìm các giá trị của a để đa thức sau nhận \(x = 1\) là một nghiệm:

\(A\left( x \right) = {a^2}{x^{2018}} + 5a{x^{2020}} - 36{x^{2022}}\)

Lời giải

I. Trắc nghiệm

Câu 1:

Phương pháp:

+ Viết đa thức dưới dạng thu gọn

+ Trong dạng thu gọn, bậc của đa thức một biến là số mũ lớn nhất của biến trong đa thức đó

Cách giải:

Ta có số mũ cao nhất của biến trong đa thức \( - {x^8} - {x^2} + {x^9} + {x^5} - 12{x^3} - {x^9} + 10 =  - {x^8} + {x^5} - 12{x^3} - {x^2} + 10\) là 8 nên bậc của đa thức là 8

Chọn B

Câu 2:

Phương pháp:

Hình hộp chữ nhật có 12 cạnh.

Cách giải:

Hình hộp chữ nhật có 12 cạnh.

Chọn A.

Câu 3:

Phương pháp:

Tìm tất cả số khả năng có thể xảy ra và số kết quả thuận lợi cho biến cố đó.

Cách giải:

Có 6 kết quả có thể xảy ra.

Có một kết quả thuận lợi cho biến cố “Bạn được chọn là nữ”.

Xác suất của biến cố bạn được chọn là nam là \(\dfrac{1}{6}\) _.

Chọn D.

Câu 4:

Phương pháp:

Sử dụng tính chất tổng 3 góc trong tam giác và tia phân giác của một góc.

Cách giải:

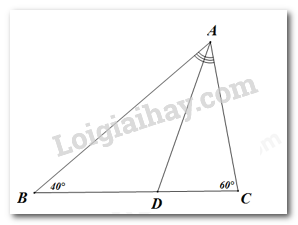
Ta có: \(\widehat {BAC} = {180^\circ }{\rm{ \;}} - \hat B - \hat C = {180^\circ }{\rm{ \;}} - {40^\circ }{\rm{ \;}} - {60^\circ }{\rm{ \;}} = {80^\circ }\)

Vì AD là tia phân giác của góc A \( \Rightarrow \widehat {BAD} = \dfrac{{\widehat {BAC}}}{2} = \dfrac{{{{80}^\circ }}}{2} = {40^\circ }\).

Chọn A.

Câu 5:

Phương pháp:

Để so sánh các cạnh của tam giác ta sử dụng định lí quan hệ về cạnh và góc trong tam giác.

Cách giải:

Vì \(DE < DF < EF{\mkern 1mu} {\mkern 1mu} (5 < 7 < 8) \Rightarrow \angle F < \angle E < \angle D\) hay \(\angle D > \angle E > \angle F\)

Chọn A.

Câu 6:

Phương pháp:

Thay lần lượt các giá trị của x vào đa thức.

Khi x = a, đa thức có giá trị bằng 0 thì a là nghiệm của đa thức.

Cách giải:

Thay \(x = {\rm{ \;}} - \dfrac{2}{5}\) vào đa thức 5x ² − 3x – 2, ta có : \(5.{\left( { - \dfrac{2}{5}} \right)^2} - 3.\left( {\dfrac{{ - 2}}{5}} \right) - 2 = 0\)

Do đó, \(x = {\rm{ \;}} - \dfrac{2}{5}\) là nghiệm của đa thức 5x ² − 3x – 2.

Chọn D.

Câu 7:

Phương pháp:

Thực hiện phép nhân 2 đa thức sau đó rút gọn.

Cách giải:

\(\begin{array}{*{20}{l}}{\left( {x - 2} \right)\left( {3x + 1} \right) - \left( { - 3x + 2} \right)\left( {1 - x} \right)}\\{ = 3{x^2} + x - 6x - 2 - \left( { - 3x + 3{x^2} + 2 - 2x} \right)}\\{ = 3{x^2} - 5x - 2 - 3{x^2} + 5x - 2}\\{ = {\rm{\;}} - 4}\end{array}\)

Chọn B.

Câu 8:

Phương pháp:

Sử dụng tính chất của tam giác cân.

Sử dụng định lý tổng ba góc trong một tam giác.

Cách giải:

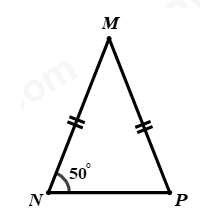
Tam giác MNP cân tại \(M \Rightarrow \angle N = \angle P = {50^0}\) (tính chất tam giác cân)

Xét \(\Delta MNP\) có: \(\angle M + \angle N + \angle P = {180^0}\) (tổng ba góc trong một tam giác)

\(\begin{array}{*{20}{l}}{ \Rightarrow \angle M + {{50}^0} + {{50}^0} = {{180}^0}}\\{ \Rightarrow \angle M + {{100}^0} = {{180}^0}}\\{ \Rightarrow \angle M = {{80}^0}}\end{array}\)

Chọn A.

II. PHẦN TỰ LUẬN (8,0 điểm)

Câu 1

Phương pháp:

+) Phân tích kỹ đầu bài, gọi số sách đóng góp cho thư viện của ba lớp 7A, 7B, 7C lần lượt là a, b, c

+) Từ dãy tỉ số bằng nhảu rút b, c theo a thế vào biểu thức từ dữ kiện đầu bài để giải tìm a, b, c

Cách giải:

Gọi số sách đóng góp cho thư viện của ba lớp 7A, 7B, 7C lần lượt là a, b, c ( a, b, c \( \in {\mathbb{N}^*}\); a , b, c < 300)

Ba lớp 7A, 7B, 7C đóng góp cho thư viện nhà trường được 300 quyển sách nên: \(a + b + c = 300\)   (1)

Số sách đóng góp cho thư viện của ba lớp 7A, 7B, 7C tỉ lệ với 5; 3; 7 nên:

\(a:b:c = 5:3:7 \Rightarrow \dfrac{a}{5} = \dfrac{b}{3} = \dfrac{c}{7}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\begin{array}{l}\dfrac{a}{5} = \dfrac{b}{3} = \dfrac{c}{7} = \dfrac{{a + b + c}}{{5 + 3 + 7}} = \dfrac{{300}}{{15}} = 20\\ \Rightarrow \left\{ \begin{array}{l}a = 20.5 = 100\;\;\;\left( {tm} \right)\\b = 20.3 = 60\;\;\;\;\;\left( {tm} \right)\\c = 20.7 = 140\;\;\;\;\left( {tm} \right)\end{array} \right..\end{array}\)

Vậy ba lớp 7A, 7B, 7C đóng góp cho thư viện lần lượt 100, 60, 140 quyển sách.

Câu 2

Phương pháp:

+ Để thu gọn đa thức ta thực hiện phép cộng các đơn thức đồng dạng.

+ Ta có thể mở rộng cộng (trừ) các đa thức dựa trên quy tắc “dấu ngoặc” và tính chất của các phép toán trên số.

+ Đối với đa thức một biến đã sắp xếp còn có thể cộng (trừ) bằng cách đặt tính theo cột dọc tương tự cộng (trừ) các số.

+ Muốn tìm nghiệm của đa thức, ta giải \(H\left( x \right) = 0\).

Cách giải:

a) Ta có:

\(\begin{array}{*{20}{l}}{A\left( x \right) = 9 - {x^5} + 2{x^3} - 10{x^4} + 3{x^2} + 3{x^4} - 2{x^2} - 4x}\\{ = {\rm{ \;}} - {x^5} + \left( { - 10{x^4} + 3{x^4}} \right) + 2{x^3} + \left( {3{x^2} - 2{x^2}} \right) - 4x + 9}\\{ = {\rm{ \;}} - {x^5} - 7{x^4} + 2{x^3} + {x^2} - 4x + 9}\end{array}\)

\(\begin{array}{*{20}{l}}{B\left( x \right) = {x^5} - 9 + 7{x^4} - 3x - {x^2} + 5{x^3} + 6x - 3{x^3}}\\{ = {x^5} + 7{x^4} + \left( {5{x^3} - 3{x^3}} \right) - {x^2} + \left( { - 3x + 6x} \right) - 9}\\{ = {x^5} + 7{x^4} + 2{x^3} - {x^2} + 3x - 9}\end{array}\)

b) Ta có:

\(\begin{array}{*{20}{l}}{A\left( x \right) + B\left( x \right) = ( - {x^5} - 7{x^4} + 2{x^3} + {x^2} - 4x + 9) + \left( {{x^5} + 7{x^4} + 2{x^3} - {x^2} + 3x - 9} \right)}\\{ = \left( { - {x^5} + {x^5}} \right) + \left( { - 7{x^4} + 7{x^4}} \right) + \left( {2{x^3} + 2{x^3}} \right) + \left( {{x^2} - {x^2}} \right) + \left( {-4x + 3x} \right) + \left( {9 - 9} \right)}\\{ = 4{x^3} -x}\end{array}\)

\(\begin{array}{*{20}{l}}{A\left( x \right) - B\left( x \right) = ( - {x^5} - 7{x^4} + 2{x^3} + {x^2} - 4x + 9) - \left( {{x^5} + 7{x^4} + 2{x^3} - {x^2} + 3x - 9} \right)}\\{ = \left( { - {x^5} - {x^5}} \right) + \left( { - 7{x^4} - 7{x^4}} \right) + \left( {2{x^3} - 2{x^3}} \right) + \left( {{x^2} + {x^2}} \right) - \left( {4x - 3x} \right) + \left( {9 + 9} \right)}\\{ = {\rm{ \;}} - 2{x^5} - 14{x^4} + 2{x^2} - 7x + 18}\end{array}\)

c) Ta có:

\(\begin{array}{*{20}{l}}{H\left( x \right) = A\left( x \right) + B\left( x \right) = 0 \Rightarrow 4{x^3} - x = 0}\\{ \Rightarrow x.\left( {4{x^2} - 1} \right) = 0}\end{array}\)

\( \Rightarrow x = 0\) hoặc \(4{x^2} -1 = 0\) \( \Rightarrow x = 0\) hoặc \({x^2} = \frac{1}{4}\) \( \Rightarrow x = 0\) hoặc \(x = \pm  \frac{1}{2}\)

Vậy \(x \in \left\{0; \pm  \frac{1}{2}\right\} \) là nghiệm của đa thức \(H\left( x \right)\).

Câu 3:

Phương pháp:

a) Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền góc nhọn, bằng cách chỉ ra hai cạnh huyền tương ứng bằng nhau, hai góc nhọn tương ứng bằng nhau.

b) Xét hai tam giác \({\Delta}ADH;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\Delta}IKH\) chứng minh hai tam giác này bằng nhau, rồi suy ra \(IK = AD\)(hai cạnh tương ứng bằng nhau)

c) Chứng minh \(DK;{\mkern 1mu} AI\) cùng vuông góc với BH

d) Nhớ lại:  trực tâm của tam giác là giao của ba đường cao. Ta chứng minh hai đường cao của tam giác HBC cắt nhau tại N.

Cách giải:

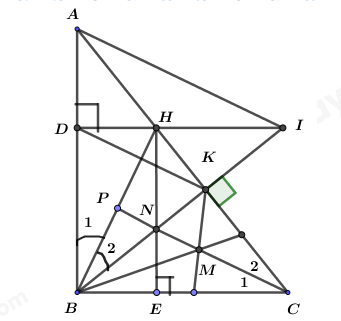
a) \(\Delta BHK = \Delta BHD\)

Vì BK là đường cao của tam giác \(\Delta ABC\) nên \(BK \bot AC\)

Xét hai tam giác vuông BHK và \(\Delta BHD\) ta có :

\(\angle {B_1} = \angle {B_2}\) (do BH là đường phân giác của góc \(\angle ABK\left( {H \in AC} \right).\))

Cạnh BH chung

\( \Rightarrow \Delta BHK = \Delta BHD\) (cạnh huyền-góc nhọn)

b) Gọi giao điểm của DH và BK là \(I\) . Chứng minh : \(IK = AD.\)

Vì \(\Delta BHK = \Delta BHD\)nên \(HK = HD\) (cạnh tương ứng)

Xét \({\Delta }ADH;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\Delta }IKH\)

Có: \(\angle DHA = \angle KHI\) (đối đỉnh)

\(HK = HD\)(cmt)

\(\angle ADH = \angle IKH = {90^0}\)

\( \Rightarrow {\Delta }ADH = {\mkern 1mu} {\mkern 1mu} {\Delta }IKH\) (g.c.g)

\(IK = AD\) (cạnh tương ứng)

c) Chứng minh \(DK//AI\)

Trong tam giác ABC có:

\(\begin{array}{*{20}{l}}{AB = AD + DB}\\{BI = BK + KI}\end{array}\)

Mà \(AD = IK{\mkern 1mu} \) (do \(\Delta ADH = \Delta IKH\left( {cmt} \right)\) )

\(DB = BK\)(do \(\Delta BHK = \Delta BHD\))

\( \Rightarrow AB = BI\)

\( \Rightarrow \Delta ABI\) là tam giác cân tại B. \( \Rightarrow \angle BAI = \angle BIA\)

Trong một tam giác cân, tia phân giác ứng với cạnh đáy chính là đường cao

\( \Rightarrow BH \bot AI{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)

Mà \(\Delta BDK\) cũng cân tại B (do \(BD = BK\left( {do{\mkern 1mu} \Delta BDH = \Delta BKH} \right)\)

\( \Rightarrow BH \bot DK{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)\) (do BH là đường phân giác góc B)

Từ (1) và (2) \( \Rightarrow DK//AI\) (do cùng vuông góc với BH ). Vậy \(DK//AI\) (đpcm).

d) Xét tam giác HBC ta có:\(BK \bot HC\left( {Gt} \right) \Rightarrow BK\) là đường cao xuất phát từ đỉnh \(B\) của tam giác HBC.

Ta có :

\(\begin{array}{*{20}{l}}{DI \bot AB\left( {GT} \right)}\\{BC \bot AB\left( {gt} \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}  \Rightarrow \angle DIB = \angle KBC{\mkern 1mu} \left( {so{\mkern 1mu} le{\mkern 1mu} trong} \right)}\\{ \Rightarrow DI//BC}\end{array}\)

Mà :

\(\begin{array}{*{20}{l}}{\angle C + \angle KBC = {{90}^0}}\\{\angle DBI + \angle DIB = {{90}^0}}\\{ \Rightarrow \angle C = \angle DBI}\\{ \Rightarrow \angle {B_1} = \angle {B_2} = \angle {C_1} = \angle {C_2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)}\end{array}\)

Kéo dài CN cắt BH tại P, ta chứng minh CP là đường cao kẻ từ đỉnh C của tam giác HBC

Ta có : \(\begin{array}{*{20}{l}}{\angle C + \angle KBC = {{90}^0}}\\{\angle {C_1} + \angle {C_2} + \angle KBC = {{90}^0}}\end{array}\)

Mà \(\angle {C_2} = \angle {B_2}{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right) \Rightarrow \angle {C_1} + \angle KBC + \angle {B_2} = \angle BPC = {90^0}\) Hay \(CP \bot CH\)

Trong tam giác HBC có : CN là đường cao, BN là đường cao. \( \Rightarrow \) N là trực tâm của \(\Delta HBC\) (đpcm).

Câu 4

Phương pháp:

\(x = a\) được gọi là nghiệm của \(P\left( x \right)\) nếu: \(P\left( a \right) = 0\)

Cách giải:

\(A\left( x \right)\) nhận \(x = {\rm{\;}} - 1\) là một nghiệm, nên \(A\left( { - 1} \right) = 0\).

Ta có: \(A\left( { - 1} \right) = {a^2}.{\left( { - 1} \right)^{2018}} + 5a.{\left( { - 1} \right)^{2020}} - 36.{\left( { - 1} \right)^{2022}} = {a^2} + 5a - 36 = 0\)

\( \Leftrightarrow {a^2} - a + 6a - 36 = 0\)

\( \Leftrightarrow a.a - a.1 + 6.a - 6.6 = 0\)

\( \Leftrightarrow a\left( {a - 1} \right) + 6\left( {a - 1} \right) = 0\)

\( \Leftrightarrow \left( {a - 1} \right)\left( {a + 6} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a - 1 = 0}\\{a + 6 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a = 1}\\{a = {\rm{\;}} - 6}\end{array}} \right.\)

Vậy \(a\) nhận các giá trị \(a = 1\)hoặc \(a = {\rm{\;}} - 6\).