Đề thi khảo sát chất lượng đầu năm Toán 6 Kết nối tri thức - Đề số 10 — Không quảng cáo

Thể tích nước khi bể đầy nước chính là thể thể tích của hình hộp chữ nhật có chiều dài $2,5m$ ; chiều rộng $1,5m$ và chiều cao $1,8m$.

Để giải bài ta có thể làm như sau:

- Tính thể tích bể nước đó theo công thức: Thể tích = Chiều dài × chiều rộng × chiều cao.

- Đổi thể tích từ đơn vị mét khối sang đơn vị đề-xi-mét khối rồi tính số lít nước.

- Tính số giờ bơm nước vào bể ta lấy thể tích khi bể đầy nước chia cho số lít nước chảy vào bể trong \(1\) giờ.

Thể tích của bể nước là:

\(2,5 \times 1,5 \times 1,8 = 6,75({m^3})\)

Đổi \(6,75{m^3} = 6750d{m^3} = 6750\) lít

Bể đầy nước sau số giờ là:

\(6750:750 = 9\) (giờ)

Đáp số: \(9\) giờ.

Vậy đáp án đúng điền vào ô trống là \(9\).

C. \(675\,d{m^2}\)

Độ dài đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đo, \(5m = 50dm\), sau đó tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho \(2\).

Đổi \(5m = 50dm\)

Diện tích tam giác đó là:

\(\dfrac{{50 \times 27}}{2} = 675\left( {d{m^2}} \right)\)

Đáp số: \(675d{m^2}\)

- Áp dụng tính chất giao hoán và kết hợp của phép nhân số thập phân.

- Nhận thấy \(0,25 \times 40 = 10{\rm{ }};\;{\rm{ }}2 \times 0,5\,{\rm{  = }}1\) nên ta nhóm \(0,25\) và \(40\) với nhau, nhóm \(2\) và \(0,5\) với nhau.

\(\begin{array}{l}18,34 \times 0,25 \times 2 \times 40 \times 0,5\\ = 18,34 \times (0,25 \times 40) \times (2 \times 0,5)\\ = 18,34 \times 10 \times 1\\ = 183,4 \times 1\\ = 183,4\end{array}\)

Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái qua phải, từ trên xuống dưới là

\(40\,;\,\,\,0,5\,;\,\,10\,;\,\,1\,;\,\,183,4\,;\,\,1\,;\,\,183,4\).

A. \(2\) ngày

+ Để làm xong một công việc, càng có nhiều người thì thời gian hoàn thành công việc đó càng giảm. Vậy đây là bài toán tỉ lệ nghịch.

+ Với dạng bài về quan hệ tỉ lệ, ta có thể làm theo 2 cách sau:

Cách 1: Dùng phương pháp rút về đơn vị.

Cách 2: Dùng phương pháp tìm tỉ số:  số người tăng lên bao nhiêu lần thì số ngày làm phải giảm đi bấy nhiêu lần.

Tóm tắt:

\(14\) người : \(5\) ngày

\(35\) người : … ngày?

(Phương pháp rút về đơn vị)

Một người làm xong công việc đó trong số ngày là:

\(14 \times 5 = 70\)  (ngày)

Nếu có \(35\) người thì sẽ làm xong công việc đó trong số ngày là:

$70:35 = 2$  (ngày)

Đáp số: \(2\) ngày.

- Tìm số gạo tẻ cửa hàng bán được, lấy tổng số gạo trừ đi số gạo nếp.

- Tìm thương của số gạo tẻ so với tổng số gạo cửa hàng bán được viết dưới dạng số thập phân.

-  Nhân thương vừa tìm được với \(100\)  được kết quả ta viết thêm kí hiệu $\% $ vào bên phải.

Cửa hàng bán được số ki-lô-gam gạo tẻ là:

\(250 - 45 = 205(kg)\)

Tỉ số phần trăm giữa số gạo tẻ và tổng số gạo cửa hàng bán được là:

\(205:250 = 0,82 = 82\% \)

Đáp số: \(82\% \).

Vậy số thích hợp điền vào ô trống là \(82\).

A. $7450000$ đồng

Coi giá vốn của chiếc ti vi là \(100\% \) thì tiền lãi sẽ chiếm \(15\% \) so với giá vốn.

Ta có:  Giá bán = giá vốn + lãi

\(115\% \)      \(100\% \)      \(15\% \)

Như vậy \(115\% \) giá vốn của chiếc ti vi là $8567500$ đồng, muốn tìm giá vốn của chiếc ti vi ta lấy  $8567500$ chia cho \(115\) rồi nhân với \(100\).

Coi giá vốn của chiếc ti vi là \(100\% \).

Giá bán của chiếc ti vi chiếm số phần trăm so với giá vốn là:

\(100\%  + 15\%  = 115\% \) giá vốn

Giá vốn của chiếc ti vi đó là:

\(8567500:115 \times 100 = 7450000\) (đồng)

Đáp số: \(7450000\) đồng.

A. \(4,8267\)

- Xác định hai đơn vị đo diện tích đã cho (\(d{m^2}\) và \(m{m^2}\)) và tìm mối liên hệ giữa chúng:

\(1d{m^2} = 10000m{m^2}\) hay \(1m{m^2} = \dfrac{1}{{10000}}d{m^2}\).

- Đổi $48267m{m^2} = 40000m{m^2} + 8267m{m^2}$, rồi đổi số đo diện tích đã cho thành hỗn số có phần phân số là phân số thập phân.

- Đổi hỗn số vừa tìm được thành số thập phân.

Ta có:

\(\begin{array}{l}48267m{m^2} \\= 40000m{m^2} + 8267m{m^2} \\= 4d{m^2} + 8267m{m^2}\\ = 4\dfrac{{8267}}{{10000}}d{m^2} \\= 4,8267d{m^2}\end{array}\)

Vậy $48267m{m^2} = 4,8267d{m^2}$.

Theo đề bài, hai ô tô xuất phát cùng lúc. Để giải bài này ta làm như sau:

- Đổi số đo thời gian sang dạng số thập phân có đơn vị là giờ.

- Tính hiệu vận tốc hai ô tô ta lấy quãng đường chia cho thời gian đi để gặp nhau.

- Khi đó ta có bài toán tìm hai số khi biết hiệu và tỉ số. Theo đề bài, vận tốc ô tô gấp đôi vận tốc xe máy nên ta vẽ sơ đồ biểu thị vận tốc xe máy là \(1\) phần thì vận tốc ô tô là \(2\) phần như thế. Coi vận tốc xe máy là số bé, vận tốc ô tô là số lớn, ta tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc

Số lớn =  Giá trị một phần × số phần của số lớn.

Đổi \(2\) giờ \(48\) phút \( = \,2,8\) giờ

Hiệu vận tốc hai xe là:

\(98:2,8 = 35\) (km/giờ)

Ta có sơ đồ:

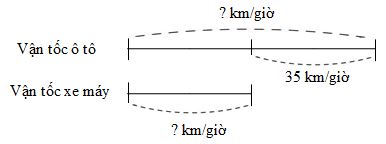
Hiệu số phần bằng nhau là:

\(2 - 1 = 1\) (phần)

Giá trị một phần hay vận tốc xe máy là:

\(35:1 \times 1 = 35\) (km/giờ)

Vận tốc ô tô là

\(35 \times 2 = 70\) (km/giờ)

Đáp số: Vận tốc ô tô: \(70\) km/giờ;

Vận tốc xe máy: \(35\) km/giờ.

Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(70\,;\,\,35\).

- Tính giá trị hai vế: biểu thức có chứa phép nhân, phép cộng, phép trừ nên ta tính phép nhân trước, phép cộng, phép trừ sau. Khi biểu thức chỉ chứa phép cộng và phép trừ, ta tính lần lượt từ trái sang phải.

- So sánh hai kết quả vừa tìm được.

Ta có:

\(\begin{array}{l}654 - 4,85 \times 68 + 506,1 &  &  & 38,3 \times 24 - 254 \times 0,35\\ = 654 - 329,8 + 506,1 &  &  &  = 919,2 - 88,9\\ = 324,2 + 506,1 &  &  &  = 830,3\\ = 830,3\end{array}\)

Mà \(830,3 = 830,3\)

Do đó: \(654 - 4,85 \times 68 + 506,1 = 38,3 \times 24 - 254 \times 0,35 \)

Vậy dấu thích hợp điền vào ô trống là \( = \).

C. \(75\)

Muốn chia một số tự nhiên cho một số thập phân ta làm như sau:

- Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì viết thêm vào bên phải số bị chia bấy nhiêu chữ số \(0\).

- Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia các số tự nhiên.

Đặt tính và thực hiện phép chia ta như sau:

- Phần thập phân của số \(0,24\) có một chữ số.

- Viết thêm hai chữ số \(0\) vào bên phải số \(18\) được \(1800\); bỏ dấu phẩy ở số \(0,24\) được \(24\).

- Thực hiện phép chia \(1800:24\).

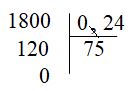
Vậy \(18:0,24 = 75\).

A. \(2,25\) giờ

- Tính vận tốc của ca nô đi từ B ta lấy vận tốc ca nô đi từ A trừ đi \( \,4\) km/giờ.

- Tính tổng vận tốc hai xe.

- Thời gian đi để gặp nhau = quãng đường : tổng vận tốc hai xe.

Vận tốc của ca nô đi từ B đến A là:

\(36 - 4 = 32\) (km/giờ)

Tổng vận tốc hai ca nô là:

\(36 + 32 = 68\) (km/giờ)

Kể từ khi khởi hành, hai ca nô gặp nhau sau khi đi số giờ là:

\(153:68 = 2,25\) (giờ)

Đáp số: \(2,25\) giờ.

B. \(1\) giờ \(38\) phút

- Ta  thực hiện tính giá trị biểu thức như đối với các số tự nhiên, tính lần lượt trong ngoặc trước ngoài ngoặc sau.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

- Trong khi tính, nếu số phút lớn hơn hoặc bằng \(60\)  thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của phút là giờ.

Ta có:

\((4\) giờ \(36\) phút  \( + \,18\) phút \()\,:\,3\)

\( = \,\,4\) giờ \(54\) phút \(\,:\,3\)

\( = \,\,3\) giờ \(114\) phút \(\,:\,3\)

\( = \,\,1\) giờ \(38\) phút

C. \(670\) viên gạch

Diện tích cần ốp gạch chính là diện tích xung quanh và diện tích một mặt đáy của cái bể.

Để giải ta có thể thực hiện các bước như sau:

- Đổi chiều dài sang đơn vị mét để ba kích thước cùng đơn vị đo.

- Tính diện tích xung quanh của cái bể ta lấy chu vi đáy nhân với chiều cao.

- Tính diện tích đáy ta lấy chiều dài nhân với chiều rộng.

- Tính diện tích cần ốp gạch ta lấy diện tích xung quanh cộng với diện tích một đáy.

- Tính diện tích một viên gạch ta lấy cạnh nhân với cạnh rồi đổi sang đơn vị diện tích là mét vuông.

- Tính số viên gạch cần dùng ta lấy diện tích cần ốp gạch chia cho diện tích một viên gạch.

Đổi \(35dm = 3,5m\)

Diện tích xung quanh của cái bể là:

\((3,5 + 2) \times 2 \times 1,8 = 19,8\;({m^2})\)

Diện tích đáy của cái bể là:

\(3,5 \times 2 = 7\;({m^2})\)

Diện tích cần ốp gạch là:

\(19,8 + 7 = 26,8\;({m^2})\)

Diện tích một viên gạch là:

\(20 \times 20 = 400\;(c{m^2})\)

Đổi \(400c{m^2} = 0,04{m^2}\)

Số viên gạch cần dùng là:

\(26,8:0,04 = 670\) (viên gạch)

Đáp số: \(670\) viên gạch.

B. Đáy lớn: \(42m\); đáy bé \(30m\)

- Tính diện tích phần đất tăng thêm.

Diện tích phần đất tăng thêm chính là diện tích hình tam giác có độ dài đáy là \(5m\) và chiều cao là chiều cao của hình thang.

- Tính chiều cao của hình thang ta lấy diện tích phần đất tăng thêm nhân với \(2\) rồi chia cho độ dài đáy \(5m\).

- Tính tổng độ dài hai đáy của hình thang ta lấy diện tích hình thang nhân với \(2\) rồi chia cho chiều cao.

- Giải bài toán tìm hai số khi biết tổng và hiệu để tìm độ dài mỗi đáy theo công thức:

Số lớn = (tổng + hiệu) \(:\,\,2\) ;  Số bé = (tổng – hiệu) \(:\,\,2\)

Ta có hình vẽ như sau:

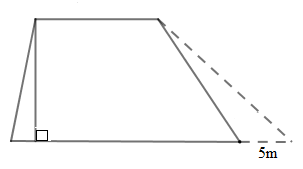
Sau khi mở rộng, diện tích miếng đất tăng thêm là:

$924 - 864 = 60\;({m^2})$

Diện tích phần đất tăng thêm chính là diện tích hình tam giác có độ dài đáy là \(5m\) và chiều cao là chiều cao của hình thang.

Chiều cao của miếng đất hình thang là:

\(60 \times 2:5 = 24\;(m)\)

Tổng độ dài hai đáy của hình thang là:

\(864 \times 2:24 = 72\;(m)\)

Độ dài đáy lớn của miếng đất đó là:

\((72 + 12):2 = 42\;(m)\)

Độ dài đáy bé của miếng đất đó là:

\(72 - 42 = 30\;(m)\)

Đáp số: đáy lớn: \(42m\); đáy bé: \(30m\).

D. \(65\% \)

- Tìm trong một giờ, cả hai vòi nước cùng chảy vào bể được bao nhiêu phần thể tích bể.

- Đổi kết quả dưới dạng phân số sang dạng phần trăm.

Cả hai vòi nước cùng chảy vào bể trong một giờ được số phần thể tích bể là:

\(\dfrac{2}{5} + \dfrac{1}{4} = \dfrac{{13}}{{20}}\) (thể tích của bể)

Ta có: \(\dfrac{{13}}{{20}} = \dfrac{{65}}{{100}} = 65\% \)

Vậy cả hai vòi nước cùng chảy vào bể trong một giờ thì được \(65\% \) thể tích của bể.

- Xác định hai đơn vị đo thể tích đã cho là \({m^3}\) và \(d{m^3}\) và tìm mối liên hệ giữa chúng: \(1{m^3} = 1000d{m^3}\).

- Đổi \(3{m^3}\) sang đơn vị đo là \(d{m^3}\), sau đó cộng thêm với \(84d{m^3}\).

Ta có \(1{m^3} = 1000d{m^3}\).

Nên \(3{m^3}\,\,84d{m^3} = \,3{m^3}\,+ 84d{m^3} = \,3000{m^3}\, + \,84\,d{m^3}\, = \,3084\,\,d{m^3}\)

Vậy đáp án đúng điền vào ô trống là \(3084\).