Đề thi vào 10 môn Toán Cần Thơ 2023 có đáp án và lời giải chi tiết — Không quảng cáo

Đề bài

A. PHẦN TRẮC NGHIỆM

Câu 1: Hàm số nào sau đây có đồ thị là hình vẽ bên dưới?

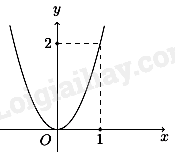
A. \(y = {\rm{ \;}} - x + 3\).

B. \(y = {\rm{ \;}} - 2{x^2}\).

C. \(y = x + 1\) .

D. \(y = 2{x^2}\).

Câu 2: Bạn Phương đặt một bức tranh hình chữ nhật có chiều rộng 0,6m và chiều dài 0,8m lên một khung hình sao cho phần còn lại của khung hình quanh bức tranh có độ rộng bằng nhau và bằng \(x\left( m \right)\) (minh họa như hình bên dưới). Biết chu vi của khung hình là 3,6m

Giá trị của x bằng

A. 0,2.

B. 0,05.

C. 0,15 .

D. 0,1.

Câu 3: Điểm nào sau đây thuộc đồ thị của hàm số \(y = {\rm{ \;}} - 7{x^2}\)?

A. \(\left( {7;1} \right)\).

B. \(\left( { - 7; - 1} \right)\).

C. \(\left( {1; - 7} \right)\) .

D. \(\left( {1;7} \right)\).

Câu 4: Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 3y = 5}\\{2x - y = 3}\end{array}} \right.\) là

A. \(\left( { - 1; - 2} \right)\).

B. \(\left( {2;1} \right)\).

C. \(\left( {1;2} \right)\).

D. \(\left( { - 2; - 1} \right)\).

Câu 5: Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?

A. \(y = 5{x^2}\).

B. \(y = {\rm{ \;}} - 5{x^2}\).

C. \(y = 5x - 6\).

D. \(y = {\rm{ \;}} - 5x - 6\).

Câu 6: Cho hai số \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) thỏa mãn \({x_1} + {x_2} = 17\) và \({x_1}{x_2} = 72\). Khi đó, \({x_1}\) và \({x_2}\) là các nghiệm của phương trình nào sau đây?

A. \({x^2} - 17x + 72 = 0\).

B. \({x^2} + 17x + 72 = 0\).

C. \({x^2} + 17x - 72 = 0\).

D. \({x^2} - 17x - 72 = 0\).

Câu 7: Tập nghiệm của phương trình \({x^2} - 24x - 25 = 0\) là

A. \(\left\{ { - 1;25} \right\}\).

B. \(\left\{ { - 25;1} \right\}\).

C. \(\left\{ {25} \right\}\).

D. \(\left\{ { - 1} \right\}\).

Câu 8: Cho hàm số \(y = ax + b{\mkern 1mu} {\mkern 1mu} \left( {a \ne 0} \right)\) có đồ thị là đường thẳng như hình vẽ bên dưới.

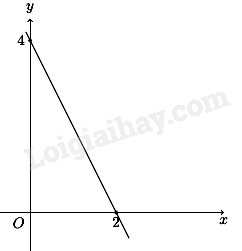
Giao điểm của đồ thị hàm số đã cho với trục hoành có tọa độ là

A. \(\left( {2;0} \right)\).

B. \(\left( {0;2} \right)\).

C. \(\left( {4;0} \right)\).

D. \(\left( {0;4} \right)\).

Câu 9: Cho hàm số \(y = x + b\) có đồ thị đi qua điểm \(A\left( {3; - 4} \right)\). Giá trị của \(b\) bằng

A. \( - 1\).

B. \(1\).

C. \( - 7\).

D. \(7\).

Câu 10: Cho đường tròn \(\left( O \right)\) bán kính \(R = 9cm\) và đường thẳng \(d\) cắt \(\left( O \right)\) tại hai điểm phân biệt \(A,{\mkern 1mu} {\mkern 1mu} B\). Biết khoảng cách từ O đến đường thẳng d bằng 8cm (minh họa như hình bên dưới).

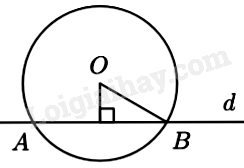
Độ dài của dây AB bằng

A. 17cm.

B. \(2\sqrt {17} cm\).

C. \(\sqrt {17} cm\).

D. 34cm.

Câu 11: Cho hình nón có bán kính đường tròn đáy \(r = 6cm\) và chiều cao \(h = 8cm\) (minh họa như hình bên dưới).

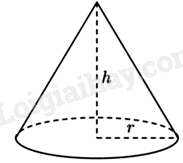
Diện tích xung quanh của hình nón đã cho bằng

A. \(96\pi c{m^2}\).

B. \(60\pi c{m^2}\).

C. \(120\pi c{m^2}\).

D. \(48\pi c{m^2}\).

Câu 12: Cho đường tròn \(\left( O \right)\) bán kính \(R = 12cm\) và đường thẳng \(d\) tiếp xúc với \(\left( O \right)\) tại điểm \(M\). Độ dài đoạn thẳng OM bằng

A. 6cm.

B. 3cm.

C. 24cm.

D. 12cm.

Câu 13: Bác Sáu có một khối gỗ dạng hình trụ với bán kính đường tròn đáy r = 3cm và chiều cao h = 8cm. Bác Sáu khoét khối gỗ đó một nửa hình cầu có bán kính đáy của khối gỗ (minh họa như hình bên dưới).

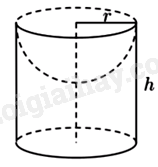
Thể tích của phần khối gỗ còn lại là

A. \(72\pi c{m^3}\).

B. \(36\pi c{m^3}\).

C. \(54\pi c{m^3}\).

D. \(108\pi c{m^3}\).

Câu 14: Đường thẳng nào sau đây song song với đường thẳng \(y = 6x + 7\)?

A. \(y = 6x - 7\).

B. \(y = 6x + 7\).

C. \(y = 7x + 6\).

D. \(y = 7x - 6\).

Câu 15: Cho tứ giác MNPQ nội tiếp đường tròn \(\left( O \right)\) (minh họa như hình bên dưới)

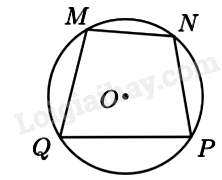
Số đo của \(\angle M + \angle P\) bằng

A. \({360^0}\).

B. \({180^0}\).

C. \({90^0}\).

D. \({270^0}\).

Câu 16: Từ chân C của một tòa nhà cao 45m nhìn lên một góc \({40^0}\) thấy ngọn B của một cây AB và từ đỉnh D của tòa nhà này nhìn xuống một góc \({50^0}\) cũng thấy ngọn B của cây đó (minh họa như hình bên dưới).

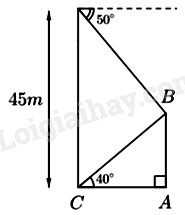
Chiều cao của cây AB (làm tròn đến chữ số thập phân thứ nhất) là

A. 20,4m.

B. 22,2m.

C. 26,4m.

D. 18,6m.

Câu 17: Hai bạn Phúc và Hồng đến một nhà sách để mua bút và vở, Bạn Phúc mua x cây bút loại I và y cây bút loại II với tổng số tiền là 96000 đồng. Bạn Hồng mua x quyển vở loại I và y quyển vở loại II với tổng số tiền là 124000 đồng. Giá bán của một cây bút và một quyển vở được cho bởi bảng sau:

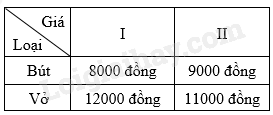
Giá trị của \(x,{\mkern 1mu} {\mkern 1mu} y\) là

A. \(x = 3,{\mkern 1mu} {\mkern 1mu} y = 8\).

B. \(x = 4,{\mkern 1mu} {\mkern 1mu} y = 7\).

C. \(x = 5,{\mkern 1mu} {\mkern 1mu} y = 6\).

D. \(x = 2,{\mkern 1mu} {\mkern 1mu} y = 9\).

Câu 18: Điều kiện của x để biểu thức \(\sqrt {x + 8} \) có nghĩa là

A. \(x \le 8\).

B. \(x \ge {\rm{ \;}} - 8\).

C. \(x \ge 8\).

D. \(x \le {\rm{ \;}} - 8\).

Câu 19: Cho đường tròn \(\left( O \right)\) có hai dây \(MN,{\mkern 1mu} {\mkern 1mu} PQ\). Hai đường thẳng \(MN,{\mkern 1mu} {\mkern 1mu} PQ\) cắt nhau tại điểm I (minh họa như hình bên dưới). Biết \(\text{sđ}\overset\frown{NnQ}={{80}^{0}}\text{,sđ}\overset\frown{MmP}={{40}^{0}}\).

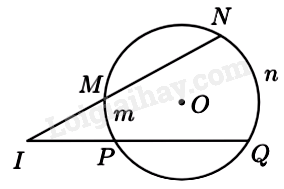
Số đo của \(\angle NIQ\) bằng

A. \({10^0}\).

B. \({60^0}\).

C. \({40^0}\).

D. \({20^0}\).

Câu 20: Gọi \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) là hai nghiệm của phương trình \({x^2} + 8x - 9 = 0\). Giá trị của \({x_1} + {x_2}\) bằng

A. 9.

B. - 9.

C. - 8.

D. 8.

Phần II. Tự luận

Câu 1: Giải phương trình và hệ phương trình sau:

a) \(3{x^2} + 5x - 12 = 0\)

b) \(\left\{ {\begin{array}{*{20}{l}}{2x - y = 7}\\{x + 2y = 6}\end{array}} \right.\)

Câu 2:

a) Rút gọn biểu thức \(Q = \frac{{\sqrt 6 {\rm{ \;}} - 2\sqrt {18} }}{{\sqrt 6 }} - {\left( {\sqrt 3 {\rm{ \;}} - 1} \right)^2}\)

b) Trên mặt phẳng tọa độ Oxy, vẽ đồ thị của hàm số \(y = \frac{3}{2}{x^2}\)

Câu 3:

a) Một phòng giáo dục và đào tạo phát động phong trào “Học sinh quyên góp sách giáo khoa lớp 9” nhằm giúp học sinh lớp 9 có hoàn cảnh khó khăn. Hưởng ứng phòng trào trên, tổng số học sinh tham gia của Trường Trung học cơ sở A và Trường trung học cơ sở B là 322. Mỗi học sinh của Trường Trung học cơ sở A quyên góp 6 quyển sách, mỗi học sinh của Trường Trung học cơ sở B quyên góp 5 quyển sách. Tổng số sách quyên góp của Trường Trung học cơ sở A nhiều hơn tổng số sách quyên góp của Trường Trung học cơ sở B là 172 quyển. Hỏi mỗi trường đã quyên góp được bao nhiêu quyển sách giáo khoa?

b) Tìm tất cả giá trị của tham số m sao cho phương trình \({x^2} - \left( {2m + 1} \right)x + {m^2} + 1 = 0\) có hai nghiệm phân biệt \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) thỏa mãn \({\left( {{x_1} + 1} \right)^2} + {\left( {{x_2} + 1} \right)^2} = 13\)

Câu 4: Cho tam giác \(ABC\left( {AB < AC} \right)\) có ba góc nhọn, nội tiếp đường tròn tâm O. Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt đường thẳng BC tại K. Từ O kẻ OD vuông góc với BC tại D, tia OD cắt đường tròn \(\left( O \right)\) tại E.

a) Chứng minh tứ giác KDOA nội tiếp.

b) Đường thẳng AE cắt BC tại N. Chứng minh tam giác KNA cân và \(K{N^2} = KB.KC\)

c) Kẻ tiếp tuyến KM của đường tròn \(\left( O \right)\) (M là tiếp điểm). Chứng minh tia MN và tia ED cắt nhau tại một điểm thuộc đường tròn \(\left( O \right)\).

-----HẾT-----

Lời giải chi tiết

Phần I: Trắc nghiệm

Câu 1 (NB)

Phương pháp:

Dựa vào dáng điệu hàm số và điểm đồ thị hàm số đi qua

Cách giải:

Ta thấy đồ thị có dạng của đồ thị hàm số bậc 2

Hơn nữa đồ thị hàm số đi qua \(\left( {1;2} \right)\) nên \(y = 2{x^2}\)

Chọn D

Chọn D.

Câu 2 (TH)

Cách giải:

Chiều rộng của khung hình là \(0,6 + 2x\,\,\left( m \right)\)

Chiều dài của khung hình là \(0,8 + 2x\,\,\left( m \right)\)

Vì chu vi của khung hình là \(3,6m\) nên

\(\begin{array}{l}2\left( {0,6 + 2x + 0,8 + 2x} \right) = 3,6\\ \Leftrightarrow 4x + 1,4 = 1,8\\ \Leftrightarrow 4x = 0,4\\ \Leftrightarrow x = 0,1\end{array}\)

Chọn D

Chọn D.

Câu 3 (NB)

Phương pháp:

Thay tọa độ từng điểm vào hàm số

Cách giải:

Ta có: \( - {7.1^2} =  - 7\)

Do đó điểm \(\left( {1; - 7} \right)\) thuộc đồ thị hàm số

Chọn C

Chọn C.

Câu 4 (NB)

Phương pháp:

Giải hệ phương trình

Cách giải:

Ta có: \(\left\{ \begin{array}{l}x + 3y = 5\\2x - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 6y = 10\\2x - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7y = 7\\2x - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\2x - 1 = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)

Chọn B

Chọn B.

Câu 5 (TH)

Phương pháp:

Hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) đồng biến trên \(\mathbb{R}\) khi \(a > 0\)

Cách giải:

Hàm số \(y = 5x - 6\) đồng biến trên \(\mathbb{R}\)

Chọn C

Chọn C.

Câu 6 (TH)

Phương pháp:

Cho hai số \({x_1},\,\,{x_2}\) thỏa mãn \({x_1} + {x_2} = S\) và \({x_1}{x_2} = P\). Khi đó, \({x_1}\) và \({x_2}\) là các nghiệm của phương trình \({x^2} - Sx + P = 0\)

Cách giải:

\({x_1}\) và \({x_2}\) là các nghiệm của phương trình \({x^2} - 17x + 72 = 0\)

Chọn A

Chọn A.

Câu 7 (TH)

Phương pháp:

Giải phương trình

Cách giải:

Ta có: \({x^2} - 24x - 25 = 0 \Leftrightarrow \left( {x + 1} \right)\left( {x - 25} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 25\end{array} \right.\)

Chọn A

Chọn A.

Câu 8 (TH)

Phương pháp:

Dựa vào đồ thị

Cách giải:

Ta thấy giao điểm của đồ thị hàm số đã cho với trục hoành có tọa độ là \(\left( {2;0} \right)\)

Chọn A

Chọn A.

Câu 9 (TH)

Phương pháp:

Thay tọa độ của điểm vào để tìm \(b\)

Cách giải:

Vì đồ thị hàm số đi qua \(A\left( {3; - 4} \right)\) nên \( - 4 = 3 + b \Rightarrow b =  - 7\)

Chọn C

Chọn C.

Câu 10 (TH)

Phương pháp:

Sử dụng định lí Pythagore

Cách giải:

Gọi \(H\) là chân đường vuông góc của \(O\) trên \(AB\)

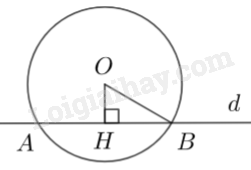
Áp dụng định lí Pythagore ta có: \(OH = \sqrt {O{B^2} - O{H^2}}  = \sqrt {{9^2} - {8^2}}  = \sqrt {17} \)

Khi đó \(AB = 2OH = 2\sqrt {17} \,\,\left( {cm} \right)\)

Chọn B

Chọn B.

Câu 11 (TH)

Phương pháp:

Diện tích xung quanh của hình nón có chiều cao \(h\) và bán kính đáy \(r\) là \(\pi r\sqrt {{r^2} + {h^2}} \)

Cách giải:

Diện tích xung quanh của hình nón có chiều cao \(h\) và bán kính đáy \(r\) là

\({S_{xq}} = \pi r\sqrt {{r^2} + {h^2}}  = \pi .6.\sqrt {{6^2} + {8^2}}  = 60\pi \left( {c{m^2}} \right)\)

Chọn B

Chọn B.

Câu 12 (TH)

Phương pháp:

Độ dài bán kính

Cách giải:

Vì đường thẳng \(d\) tiếp xúc với \(\left( O \right)\) tại điểm \(M\) nên \(OM = R = 12\left( {cm} \right)\)

Chọn D

Chọn D.

Câu 13 (TH)

Phương pháp:

- Tính thể tích của khối trụ

- Tính thể tích của nửa khối cầu

Cách giải:

Thể tích của khối trụ là \(V = \pi {r^2}h = \pi {.3^2}.8 = 72\pi \,\,\left( {c{m^3}} \right)\)

Thể tích của nửa khối cầu là \({V_1} = \frac{1}{2}.\frac{4}{3}\pi {r^3} = \frac{2}{3}\pi {.3^3} = 18\pi \,\,\left( {c{m^3}} \right)\)

Thể tích khối gỗ còn lại là \({V_2} = V - {V_1} = 72\pi  - 18\pi  = 54\pi \,\,\left( {c{m^3}} \right)\)

Chọn C

Chọn C.

Câu 14 (NB)

Phương pháp:

Giải phương trình

Cách giải:

Đường thẳng song song với đường thẳng \(y = 6x + 7\) là \(y = 6x - 7\)

Chọn A

Chọn A.

Câu 15 (NB)

Phương pháp:

Tổng của 2 góc đối trong tứ giác nội tiếp

Cách giải:

Ta có: \(\angle M + \angle P = {180^0}\)

Chọn B

Chọn B.

Câu 16 (TH)

Phương pháp:

- Dựa vào định lí cosin tính \(BC\)

- Dựa vào đính lí sin tính \(AB\)

Cách giải:

Ta có: \(\angle BCD + \angle ACB = {90^0} \Rightarrow \angle BCD + {40^0} = {90^0} \Rightarrow \angle BCD = {50^0}\)

Tương tự ta có \(\angle BDC = {40^0}\)

Do đó \(\angle DBC = {90^0}\) hay \(\Delta BCD\) vuông tại \(B\)

Khi đó \(\cos \angle BCD = \frac{{BC}}{{CD}} \Rightarrow BC = CD.\cos {50^0} = 45\cos {50^0}\)

\(\Delta ABC\) vuông tại \(A\) nên \(\sin \angle ACB = \frac{{AB}}{{BC}} \Rightarrow AB = BC\sin {40^0} = 45\cos {50^0}\sin {40^0} \approx 18,6\,\,\left( m \right)\)

Chọn D

Chọn D.

Câu 17 (TH)

Phương pháp:

Lập hệ phương trình

Cách giải:

Từ giả thiết ta có hệ phương trình \(\left\{ \begin{array}{l}8000x + 9000y = 96000\\12000x + 11000y = 124000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8x + 9y = 96\\12x + 11y = 124\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 8\end{array} \right.\)

Chọn A

Chọn A.

Câu 18 (TH)

Cách giải:

Biểu thức có nghĩa khi \(x + 8 \ge 0 \Leftrightarrow x \ge  - 8\)

Chọn B

Chọn B.

Câu 19 (TH)

Phương pháp:

Số đo của góc có đỉnh nằm ngoài đường tròn bằng nửa hiệu của số đo của hai cung bị chắn

Cách giải:

Ta có: \(\angle NIQ=\frac{\text{sđ}\overset\frown{NnQ}-\text{sđ}\overset\frown{MmP}}{2}=\frac{{{80}^{0}}-{{40}^{0}}}{2}={{20}^{0}}\)

Chọn D

Chọn D.

Câu 20 (TH)

Phương pháp:

Sử dụng định lí Viete

Cách giải:

Theo định lí Viete ta có: \({x_1} + {x_2} =  - 8\)

Chọn C

Chọn C.

B. TỰ LUẬN

Câu 1 (TH)

Phương pháp:

Giải phương trình, hệ phương trình

Cách giải:

a) \(3{x^2} + 5x - 12 = 0\)

\(\begin{array}{l} \Leftrightarrow 3{x^2} + 9x - 4x - 12 = 0\\ \Leftrightarrow 3x\left( {x + 3} \right) - 4\left( {x + 3} \right) = 0\\ \Leftrightarrow \left( {3x - 4} \right)\left( {x + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}3x - 4 = 0\\x + 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{4}{3}\\x =  - 3\end{array} \right.\end{array}\)

b) \(\left\{ \begin{array}{l}2x - y = 7\\x + 2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = 7\\2x + 4y = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = 7\\5y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 1 = 7\\y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 1\end{array} \right.\)

Câu 2 (TH)

Cách giải:

a)

\(\begin{array}{l}Q = \frac{{\sqrt 6  - 2\sqrt {18} }}{{\sqrt 6 }} - {\left( {\sqrt 3  - 1} \right)^2}\\\,\,\,\,\, = \frac{{\sqrt 6  - 2\sqrt 3 .\sqrt 6 }}{{\sqrt 6 }} - \left( {3 - 2\sqrt 3  + 1} \right)\\\,\,\,\,\, = \frac{{\sqrt 6 \left( {1 - 2\sqrt 3 } \right)}}{{\sqrt 6 }} - \left( {4 - 2\sqrt 3 } \right)\\\,\,\,\,\, = 1 - 2\sqrt 3  - 4 + 2\sqrt 3 \\\,\,\,\,\, =  - 3\end{array}\)

Vậy \(Q =  - 3\)

b)

Ta có bảng giá trị sau:

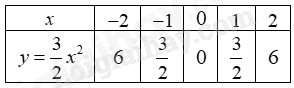
Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\left( {0;0} \right),\,\,A\left( { - 2;6} \right),\,\,B\left( { - 1;\frac{3}{2}} \right),\,\,C\left( {1;\frac{3}{2}} \right),\,\,D\left( {2;6} \right)\)

Hệ số \(a = \frac{3}{2} > 0\) nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận \(Oy\) làm trục đối xứng

Ta vẽ được đồ thị hàm số \(y = \frac{3}{2}{x^2}\) như sau:

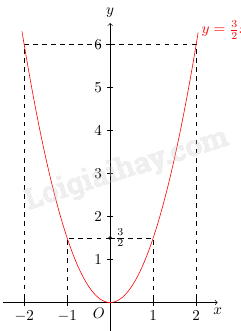
Câu 23 (TH)

Cách giải:

a) Gọi số học sinh của trường A là \(x\) (học sinh) (ĐK: \(x \in \mathbb{N}*,\,\,x < 322\))

Suy ra số học sinh của trường B là \(322 - x\) học sinh

Mỗi học sinh trường A quyên góp 6 quyển sách nên Trường A quyên góp được \(6x\) (quyển sách)

Mỗi học sinh trường B quyên góp 5 quyển sách nên Trường B quyên góp được \(5\left( {322 - x} \right)\) (quyển sách)

Vì tổng số sách quyên góp của Trường Trung học cơ sở A nhiều hơn tổng số sách quyên góp của Trường Trung học cơ sở B là 172 quyển nên

\(\begin{array}{l}6x - 5\left( {322 - x} \right) = 172\\ \Leftrightarrow 6x - 1610 + 5x = 172\\ \Leftrightarrow 11x = 1782\\ \Leftrightarrow x = 162\,\,\left( {TM} \right)\end{array}\)

Vậy trường A quyên góp được \(6.162 = 972\) (quyển sách)

Trường B quyên góp được \(972 - 172 = 800\) (quyển sách)

b) \({x^2} - \left( {2m + 1} \right)x + {m^2} + 1 = 0\)

\(\Delta  = \left[ { - {{\left( {2m + 1} \right)}^2}} \right] - 4.1.\left( {{m^2} + 1} \right) = 4{m^2} + 4m + 1 - 4{m^2} - 4 = 4m - 3\)

Để phương trình có hai nghiệm phân biệt thì \(\Delta  > 0 \Leftrightarrow 4m - 3 > 0 \Leftrightarrow m > \frac{3}{4}\)

Áp dụng định lí Viete ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = {m^2} + 1\end{array} \right.\)

Ta có: \({\left( {{x_1} + 1} \right)^2} + {\left( {{x_2} + 1} \right)^2} = 13\)

\(\begin{array}{l} \Leftrightarrow x_1^2 + 2{x_1} + 1 + x_2^2 + 2{x_2} + 1 = 13\\ \Leftrightarrow x_1^2 + x_2^2 + 2\left( {{x_1} + {x_2}} \right) - 11 = 0\\ \Leftrightarrow x_1^2 + x_2^2 + 2{x_1}{x_2} - 2{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) - 11 = 0\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) - 11 = 0\\ \Rightarrow {\left( {2m + 1} \right)^2} - 2\left( {{m^2} + 1} \right) + 2\left( {2m + 1} \right) - 11 = 0\\ \Leftrightarrow 4{m^2} + 4m + 1 - 2{m^2} - 2 + 4m + 2 - 11 = 0\\ \Leftrightarrow 2{m^2} + 8{m^2} - 10 = 0\\ \Leftrightarrow {m^2} + 4m - 5 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{m_1} = 1\,\,\left( {TM} \right)\\{m_2} =  - 5\,\,\left( {KTM} \right)\end{array} \right.\end{array}\)

Vậy \(m = 1\)

Câu 4 (VD)

Cách giải:

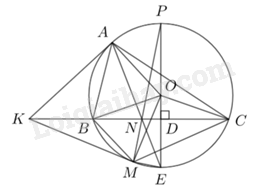
a) Do \(OD \bot BC\,\,\left( {gt} \right) \Rightarrow \angle ODK = {90^0}\)

Do \(KA\) là tiếp tuyến của \(O\,\,\left( {gt} \right)\) nên \(OA \bot KA \Rightarrow \angle OAK = {90^0}\)

\( \Rightarrow \angle ODK + \angle OAK = {90^0} + {90^0} = {180^0}\)

Mà 2 góc này ở vị trí đối diện nên tứ giác \(KDOA\) nội tiếp (dhnb) (đpcm)

b) Ta có: \(OB = OC\) (cùng bằng bán kính của \(\left( O \right)\)) nên \(\Delta OBC\) cân tại \(O\), đường cao \(OD\)

\( \Rightarrow OD\) đồng thời là phân giác (tính chất tam giác cân)

\( \Rightarrow \angle EOB = \angle EOC\)

Do đó \(\text{sđ}\overset\frown{BE}=\text{sđ}\overset\frown{CE}\) (hai góc ở tâm bằng nhau chắn hai cung bằng nhau)

Ta có: \(\angle ANK=\frac{1}{2}\left( \text{sđ}\overset\frown{AB}+\text{sđ}\overset\frown{CE} \right)=\frac{1}{2}\left( \text{sđ}\overset\frown{AB}+\text{sđ}\overset\frown{BE} \right)=\frac{1}{2}\text{sđ}\overset\frown{AE}=\angle KAE\) (tính chất góc tạo bởi tiếp tuyến và dây cung)

\( \Rightarrow \Delta AKN\) cân tại \(K\)

Xét \(\Delta KAB\) và \(\Delta KCA\) có:

\(\angle AKC\) chung

\(\angle KAB = \angle KCA\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(AB\))

\(\begin{align}\Rightarrow \Delta KAB\backsim \Delta KCA\,\,\left( g.g \right) \\ \Rightarrow \frac{KA}{KC}=\frac{KB}{KA} \\ \Rightarrow K{{A}^{2}}=KB.KC \end{align}\)

Mà \(\Delta AKN\) cân tại \(K \Rightarrow KA = KN \Rightarrow K{N^2} = KB.KC\) (đpcm)

c) Do \(KM\) là tiếp tuyến của \(\left( O \right)\) nên \(KM = KA\) (tính chất hai tiếp tuyến cắt nhau)

Mà \(KA = KN\,\,\left( {cmt} \right)\) nên \(KA = KM = KN\)

Do đó \(\Delta KMN\) cân tại \(K\)

\( \Rightarrow \angle KNM = \angle KMN\)

Ta có: \(\angle BMN = \angle KMN - \angle KMB\) và \(\angle NMC = \angle KNM - \angle KCM\) (tính chất góc ngoài tam giác \(NCM\))

Mà \(\angle KCM = \angle KMB\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(BM\))

Do đó \(\angle BMN = \angle NMC\)

Gọi \(P\) là giao điểm của \(MN\) với \(\left( O \right)\) thì \(\angle BMP = \angle CMP\)

Do đó \(\overset\frown{PB}=\overset\frown{PC}\)

\( \Rightarrow P\) là điểm chính giữa cung lớn \(BC\)

Mà \(\overset\frown{BE}=\overset\frown{CE}\,\,\left( cmt \right)\) nên \(E\) là điểm chính giữa cung nhỏ \(BC\)

\( \Rightarrow PE\) là đường trung trực của \(BC\)

Mà \(OB = OC\left( { = R} \right)\) nên \(O\) thuộc trung trực \(BC\)

Do đó \(P,\,\,E,\,\,O,\,\,D\) thẳng hàng

Vậy \(MN,\,\,ED\) cắt nhau tại một điểm \(P\) thuộc đường tròn \(\left( O \right)\)