Đề thi vào 10 môn Toán Hải Dương năm 2020
Tải vềCâu 1: 1) Giải các phương trình sau:
Đề thi
Câu 1:
1) Giải các phương trình sau:
a) \(\left| {x - 1} \right| = 8\) b) \(x\left( {2 + x} \right) - 3 = 0\)
2) Cho phương trình \({x^2} - 3x + 1 = 0\). Gọi \({x_1}\) và \({x_2}\) là hai nghiệm của phương trình. Hãy tính giá trị biểu thức \(A = x_1^2 + x_2^2\).
Câu 2:
a) Rút gọn biểu thức \(A = \left( {\dfrac{x}{{x + 3\sqrt x }} + \dfrac{1}{{\sqrt x + 3}}} \right):\left( {1 - \dfrac{2}{{\sqrt x }} + \dfrac{6}{{x + 3\sqrt x }}} \right)\) (với \(x > 0\)).
b) Viết phương trình đường thẳng đi qua điểm \(M\left( { - 1;4} \right)\) và song song với đường thẳng \(y = 2x - 1\).
Câu 3:
a) Một đoàn xe nhận chở 480 tấn hàng. Khi sắp khởi hành, đoàn có thêm 3 xe nữa nên mỗi xe chở ít hơn 8 tấn so với dự định. Hỏi lúc đầu đoàn xe có bao nhiêu chiếc? Biết rằng các xe chở khối lượng hàng bằng nhau.
b) Cho hệ phương trình với tham số \(m:\,\,\left\{ \begin{array}{l}\left( {m + 1} \right)x - y = 3\\mx + y = m\end{array} \right..\)
Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {{x_0};\,\,{y_0}} \right)\) thỏa mãn \({x_0} + {y_0} > 0.\)
Câu 4:
Cho \(\Delta ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( {O;\,\,R} \right).\) Gọi \(D,\,\,E,\,\,F\) là chân các đường cao lần lượt thuộc các cạnh \(BC,\,\,CA,\,\,AB\) và \(H\) là trực tâm của \(\Delta ABC.\) Vẽ đường kính \(AK.\)
a) Chứng minh tứ giác \(BHCK\) là hình bình hành.
b) Trong trường hợp \(\Delta ABC\) không cân, gọi \(M\) là trung điểm của \(BC.\) Hãy chứng minh \(FC\) là phân giác của \(\angle DFE\) và bốn điểm \(M,\,\,D,\,\,F,\,\,E\) cùng nằm trên một đường tròn.
c) Khi \(BC\) và đường tròn \(\left( {O;\,\,R} \right)\) cố định, điểm \(A\) thay đổi trên đường tròn sao cho \(\Delta ABC\) luôn nhọn, đặt \(BC = a.\) Tìm vị trí của điểm \(A\) để tổng \(P = DE + EF + DF\) lớn nhất và tìm giá trị lớn nhất đó theo \(a\) và \(R.\)
Câu 5:
Cho ba số thực dương \(a,\,\,b,\,\,c\) thỏa mãn \(abc = 1\).
Chứng minh rằng: \(\dfrac{1}{{{a^2} + 2{b^2} + 3}} + \dfrac{1}{{{b^2} + 2{c^2} + 3}} + \dfrac{1}{{{c^2} + 2{a^2} + 3}} \le \dfrac{1}{2}\)
Lời giải chi tiết
Câu 1 (2,0 điểm)
Cách giải:
1) Giải các phương trình sau:
a) \(\left| {x - 1} \right| = 8\) \( \Leftrightarrow \left[ \begin{array}{l}x - 1 = 8\\x - 1 = - 8\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 9\\x = - 7\end{array} \right.\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {9; - 7} \right\}\).
b) \(x\left( {2 + x} \right) - 3 = 0\)
\(\begin{array}{l} \Leftrightarrow 2x + {x^2} - 3 = 0\\ \Leftrightarrow {x^2} + 3x - x - 3 = 0\\ \Leftrightarrow \left( {{x^2} + 3x} \right) - \left( {x + 3} \right) = 0\\ \Leftrightarrow x\left( {x + 3} \right) - \left( {x + 3} \right) = 0\\ \Leftrightarrow \left( {x + 3} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\x - 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 1\end{array} \right.\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - 3;1} \right\}\).
2) Cho phương trình \({x^2} - 3x + 1 = 0\) . Gọi \({x_1}\) và \({x_2}\) là hai nghiệm của phương trình. Hãy tính giá trị biểu thức \(A = x_1^2 + x_2^2\) .
Xét phương trình \({x^2} - 3x + 1 = 0\) có \(\Delta = {\left( { - 3} \right)^2} - 4.1.1 = 5 > 0\) nên phương trình luôn có hai nghiệm phân biệt \({x_1},\,\,{x_2}\). Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - \left( { - 3} \right)}}{1} = 3\\{x_1}{x_2} = \dfrac{1}{1} = 1\end{array} \right.\).
Ta có:
\(\begin{array}{l}A = x_1^2 + x_2^2\\A = x_1^2 + x_2^2 + 2{x_1}{x_2} - 2{x_1}{x_2}\\A = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\\A = {3^2} - 2.1\\A = 7\end{array}\)
Vậy \(A = 7\).
Câu 2 (2,0 điểm)
Cách giải:
a) Rút gọn biểu thức \(A = \left( {\dfrac{x}{{x + 3\sqrt x }} + \dfrac{1}{{\sqrt x + 3}}} \right):\left( {1 - \dfrac{2}{{\sqrt x }} + \dfrac{6}{{x + 3\sqrt x }}} \right)\) (với \(x > 0\) ).
Với \(x > 0\) ta có:
\(\begin{array}{l}A = \left( {\dfrac{x}{{x + 3\sqrt x }} + \dfrac{1}{{\sqrt x + 3}}} \right):\left( {1 - \dfrac{2}{{\sqrt x }} + \dfrac{6}{{x + 3\sqrt x }}} \right)\\A = \left( {\dfrac{x}{{\sqrt x \left( {\sqrt x + 3} \right)}} + \dfrac{1}{{\sqrt x + 3}}} \right):\left( {1 - \dfrac{2}{{\sqrt x }} + \dfrac{6}{{\sqrt x \left( {\sqrt x + 3} \right)}}} \right)\\A = \left( {\dfrac{{\sqrt x }}{{\sqrt x + 3}} + \dfrac{1}{{\sqrt x + 3}}} \right):\dfrac{{\sqrt x \left( {\sqrt x + 3} \right) - 2\left( {\sqrt x + 3} \right) + 6}}{{\sqrt x \left( {\sqrt x + 3} \right)}}\\A = \dfrac{{\sqrt x + 1}}{{\sqrt x + 3}}:\dfrac{{x + 3\sqrt x - 2\sqrt x - 6 + 6}}{{\sqrt x \left( {\sqrt x + 3} \right)}}\\A = \dfrac{{\sqrt x + 1}}{{\sqrt x + 3}}:\dfrac{{x + \sqrt x }}{{\sqrt x \left( {\sqrt x + 3} \right)}}\\A = \dfrac{{\sqrt x + 1}}{{\sqrt x + 3}}:\dfrac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{\sqrt x \left( {\sqrt x + 1} \right)}}\\A = 1\end{array}\)
Vậy với \(x > 0\) thì \(A = 1\).
b) Viết phương trình đường thẳng đi qua điểm \(M\left( { - 1;4} \right)\) và song song với đường thẳng \(y = 2x - 1\) .
Gọi \(d\) là đường thẳng cần tìm.
Vì \(d\) song song với đường thẳng \(y = 2x - 1\) nên phương trình đường thẳng \(d\) có dạng \(y = 2x + c\,\,\left( {c \ne - 1} \right)\).
Vì \(M\left( { - 1;4} \right) \in d\) nên thay tọa độ điểm \(M\) vào phương trình đường thẳng \(d\) ta có:
\(4 = 2.\left( { - 1} \right) + c \Leftrightarrow 4 = - 2 + c \Leftrightarrow c = 6\,\,\left( {tm} \right)\).
Vậy phương trình đường thẳng cần tìm là \(y = 2x + 6\).
Câu 3 (2,0 điểm)
Cách giải:
a) Một đoàn xe nhận chở 480 tấn hàng. Khi sắp khởi hành, đoàn có thêm 3 xe nữa nên mỗi xe chở ít hơn 8 tấn so với dự định. Hỏi lúc đầu đoàn xe có bao nhiêu chiếc? Biết rằng các xe chở khối lượng hàng bằng nhau.
Gọi số lúc đầu của đoàn xe là \(x\) (chiếc), \(\left( {x \in {\mathbb{N}^*}} \right)\).
Lúc đầu mỗi xe chở số tấn hàng là \(\dfrac{{480}}{x}\) (tấn).
Khi khởi hành, có thêm 3 xe nên số xe lúc sau là:\(x + 3\) (xe).
Lúc đầu mỗi xe chở số tấn hàng là \(\dfrac{{480}}{{x + 3}}\) (tấn).
Vì lúc sau mỗi xe chở ít hơn 8 tấn hàng so với dự định nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\dfrac{{480}}{x} - \dfrac{{480}}{{x + 3}} = 8\\ \Leftrightarrow \dfrac{{60}}{x} - \dfrac{{60}}{{x + 3}} = 1\\ \Leftrightarrow 60\left( {x + 3} \right) - 60x = x\left( {x + 3} \right)\\ \Leftrightarrow 60x + 180 - 60x = {x^2} + 3x\\ \Leftrightarrow {x^2} + 3x - 180 = 0\\ \Leftrightarrow {x^2} + 15x - 112x - 180 = 0\\ \Leftrightarrow x\left( {x + 15} \right) - 12\left( {x + 15} \right) = 0\\ \Leftrightarrow \left( {x + 15} \right)\left( {x - 12} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 15 = 0\\x - 12 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 15\,\,\,\left( {tm} \right)\\x = 12\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy lúc đầu đoàn xe có 12 chiếc.
b) Cho hệ phương trình với tham số \(m:\,\,\left\{ \begin{array}{l}\left( {m + 1} \right)x - y = 3\\mx + y = m\end{array} \right..\)
Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {{x_0};\,\,{y_0}} \right)\) thỏa mãn \({x_0} + {y_0} > 0.\)
Ta có: \(\left\{ \begin{array}{l}\left( {m + 1} \right)x - y = 3\\mx + y = m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m + 1} \right)x - m + mx = 3\\y = m - mx\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {2m + 1} \right)x = m + 3\,\,\,\left( * \right)\\y = m - mx\end{array} \right.\)
Hệ phương trình đã cho có nghiệm duy nhất \( \Leftrightarrow \left( * \right)\) có nghiệm duy nhất \( \Leftrightarrow 2m + 1 \ne 0 \Leftrightarrow m \ne - \dfrac{1}{2}.\)
Khi đó ta có: \(\left( * \right) \Leftrightarrow x = \dfrac{{m + 3}}{{2m + 1}}\,\,\left( {m \ne - \dfrac{1}{2}} \right)\)
\(\begin{array}{l} \Rightarrow y = m - mx = m - \dfrac{{m\left( {m + 3} \right)}}{{2m + 1}}\\ \Leftrightarrow y = \dfrac{{2{m^2} + m - {m^2} - 3m}}{{2m + 1}}\\ \Leftrightarrow y = \dfrac{{{m^2} - 2m}}{{2m + 1}}\end{array}\)
\( \Rightarrow \) Với \(m \ne - \dfrac{1}{2}\) thì hệ phương trình có nghiệm duy nhất \(\left( {{x_0};\,\,{y_0}} \right) = \left( {\dfrac{{m + 3}}{{2m + 1}};\,\,\dfrac{{{m^2} - 2m}}{{2m + 1}}} \right).\)
Theo bài ra ta có: \({x_0} + {y_0} > 0\)
\(\begin{array}{l} \Leftrightarrow \dfrac{{m + 3}}{{2m + 1}} + \dfrac{{{m^2} - 2m}}{{2m + 1}} > 0\\ \Leftrightarrow \dfrac{{{m^2} - m + 3}}{{2m + 1}} > 0\,\,\,\left( 1 \right)\end{array}\)
Vì \({m^2} - m + 3 = {m^2} - 2.\dfrac{1}{2}m + \dfrac{1}{4} + \dfrac{{11}}{4}\) \( = {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{{11}}{4} > 0\,\,\forall m\)
\( \Rightarrow \left( 1 \right) \Leftrightarrow 2m + 1 > 0 \Leftrightarrow m > - \dfrac{1}{2}\)
Kết hợp với điều kiện \(m \ne - \dfrac{1}{2}\) ta được \(m > - \dfrac{1}{2}\) thỏa mãn bài toán.
Vậy \(m > - \dfrac{1}{2}.\)
Câu 4 (3,0 điểm)
Cách giải:
Cho \(\Delta ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( {O;\,\,R} \right).\) Gọi \(D,\,\,E,\,\,F\) là chân các đường cao lần lượt thuộc các cạnh \(BC,\,\,CA,\,\,AB\) và \(H\) là trực tâm của \(\Delta ABC.\) Vẽ đường kính \(AK.\)
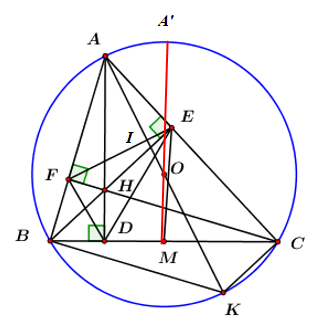
a) Chứng minh tứ giác \(BHCK\) là hình bình hành.
Ta có: \(\angle ABK\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\) \( \Rightarrow \angle ABK = {90^0}\) hay \(AB \bot BK\).
Mà \(CF \bot AB\,\,\,\left( {gt} \right)\) \( \Rightarrow CF\parallel BK\) hay \(CH\parallel BK\,\,\,\left( 1 \right)\) (Từ vuông góc đến song song).
Ta có: \(\angle ACK\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\) \( \Rightarrow \angle ACK = {90^0}\) hay \(AC \bot CK\).
Mà \(BE \bot AC\,\,\,\left( {gt} \right)\) \( \Rightarrow BE\parallel CK\) hay \(BH\parallel CK\,\,\,\left( 2 \right)\) (Từ vuông góc đến song song).
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra tứ giác \(BHCK\) là hình bình hành. (dhnb)
b) Trong trường hợp \(\Delta ABC\) không cân, gọi \(M\) là trung điểm của \(BC.\) Hãy chứng minh \(FC\) là phân giác của \(\angle DFE\) và bốn điểm \(M,\,\,D,\,\,F,\,\,E\) cùng nằm trên một đường tròn.
Xét tứ giác \(BFHD\) ta có: \(\angle BFD + \angle BHD = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow BFHD\) là tứ giác nội tiếp (dhnb).
\( \Rightarrow \angle HFD = \angle HBD\) (hai góc nội tiếp cùng chắn cung \(HD\)) \(\left( 3 \right)\)
Xét tứ giác \(AEHF\) ta có: \(\angle AEH + \angle AFH = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow AEHF\) là tứ giác nội tiếp (dhnb).
\( \Rightarrow \angle HFE = \angle HAE\) (hai góc nội tiếp cùng chắn cung \(HE\)) \(\left( 4 \right)\)
Xét tứ giác \(AEDB\) ta có: \(AEB = \angle ADB = {90^0}\)
\( \Rightarrow AEDB\) là tứ giác nội tiếp (Tứ giác có hai đỉnh liên tiếp cùng kề nhìn cạnh đối diện dưới các góc bằng nhau).
\( \Rightarrow \angle DAE = \angle DBE\) (hai góc nội tiếp cùng chắn cung \(DE\)) \(\left( 5 \right)\)
Từ \(\left( 3 \right),\,\,\left( 4 \right),\,\,\left( 5 \right)\) suy ra: \(\angle EAD = \angle EFH = \angle HFD = \angle HBD\)
Hay \(\angle EFC = \angle CFD\) \( \Rightarrow FC\) là phân giác của \(\angle DFE\) (đpcm).
Xét \(\Delta EBC\) vuông tại \(E\) có đường trung tuyến \(EM\) \( \Rightarrow EM = BM = \dfrac{1}{2}BC\)
\( \Rightarrow \Delta EBM\) cân tại \(M\) (tính chất tam giác cân).
\( \Rightarrow \angle MEB = \angle EBM\) \( \Rightarrow \angle EMC = \angle MEB + \angle EBM = 2\angle EBM\) (góc ngoài của tam giác)
Lại có: \(\angle EFD = 2\angle HFD = 2\angle HBD = 2\angle EBM\,\,\,\,\left( {cmt} \right)\)
\( \Rightarrow \angle EMC = \angle EFD\,\,\left( { = 2\angle EBM} \right)\)
\( \Rightarrow EFDM\) là tứ giác nội tiếp (Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện)
Hay \(E,\,\,F,\,\,D,\,\,M\) cùng thuộc một đường tròn.
c) Khi \(BC\) và đường tròn \(\left( {O;\,\,R} \right)\) cố định, điểm \(A\) thay đổi trên đường tròn sao cho \(\Delta ABC\) luôn nhọn, đặt \(BC = a.\) Tìm vị trí của điểm \(A\) để tổng \(P = DE + EF + DF\) lớn nhất và tìm giá trị lớn nhất đó theo \(a\) và \(R.\)
Gọi \(EF \cap OA = \left\{ I \right\}\).
Ta có: \(\angle FAI = \angle BCK\) (hai góc nội tiếp cùng chắn cung \(BK\)).
Xét tứ giác \(BFEC\) có: \(\angle BEC = \angle BFC = {90^0}\,\left( {gt} \right)\), do đó tứ giác \(BFEC\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn 1 cạnh dưới các góc bằng nhau).
\( \Rightarrow \angle AFI = \angle ACB\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
\( \Rightarrow \angle FAI + \angle AFI = \angle BCK + \angle ACB = \angle ACK = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
\( \Rightarrow OA \bot EF\).
CMTT ta có \(OB \bot FD\), \(OC \bot ED\).
Ta có: \({S_{OEAF}} = \dfrac{1}{2}OA.EF\) (tứ giác có 2 đường chéo vuông góc).
\({S_{OFBD}} = \dfrac{1}{2}OB.FD\)
\({S_{ODCE}} = \dfrac{1}{2}OC.DE\).
\(\begin{array}{l} \Rightarrow {S_{OEAF}} + {S_{OFBD}} + {S_{ODCE}} = \dfrac{1}{2}OA.EF + \dfrac{1}{2}OB.FD + \dfrac{1}{2}OC.DE\\ \Rightarrow {S_{ABC}} = \dfrac{1}{2}R.EF + \dfrac{1}{2}R.FD + \dfrac{1}{2}R.DE\\ \Rightarrow {S_{ABC}} = \dfrac{1}{2}R.\left( {EF + FD + DE} \right)\\ \Rightarrow EF + FD + DE = \dfrac{{2{S_{ABC}}}}{R}\end{array}\)
Kéo dài \(OM\) cắt \(\left( O \right)\) tại \(A'\) \( \Rightarrow A'M \bot BC\,\,\left( {do\,\,OM \bot BC} \right)\).
Khi đó ta có: \({S_{ABC}} = \dfrac{1}{2}AD.BC \le \dfrac{1}{2}A'M.BC\).
Áp dụng định í Pytago trong tam giác vuông \(OMC\) ta có: \(OM = \sqrt {O{C^2} - C{M^2}} = \sqrt {{R^2} - \dfrac{{{a^2}}}{4}} \).
\( \Rightarrow A'M = OA' + OM = R + \sqrt {{R^2} - \dfrac{{{a^2}}}{4}} \).
\( \Rightarrow {S_{ABC}} \le \dfrac{a}{2}\left( {R + \sqrt {{R^2} - \dfrac{{{a^2}}}{4}} } \right)\).
\( \Rightarrow EF + FD + DE \le \dfrac{{a\left( {R + \sqrt {{R^2} - \dfrac{{{a^2}}}{4}} } \right)}}{R}\).
Dấu “=” xảy ra \( \Leftrightarrow A \equiv A'\), khi đó điểm \(A\) là điểm chính giữa của cung lớn \(BC\).
Vậy \(P = DE + EF + DF\) đạt giá trị lớn nhất điểm \(A\) là điểm chính giữa của cung lớn \(BC\).
Câu 5 (1,0 điểm)
Cách giải:
Cho ba số thực dương \(a,\,\,b,\,\,c\) thỏa mãn \(abc = 1\) .
Chứng minh rằng: \(\dfrac{1}{{{a^2} + 2{b^2} + 3}} + \dfrac{1}{{{b^2} + 2{c^2} + 3}} + \dfrac{1}{{{c^2} + 2{a^2} + 3}} \le \dfrac{1}{2}\)
Ta có: \({a^2} + 2{b^2} + 3 = {a^2} + {b^2} + {b^2} + 1 + 2\).
Áp dụng BĐT Cô-si ta có: \(\left\{ \begin{array}{l}{a^2} + {b^2} \ge 2ab\\{b^2} + 1 \ge 2b\end{array} \right.\).
\( \Rightarrow {a^2} + {b^2} + {b^2} + 1 + 2 \ge 2ab + 2b + 2 = 2\left( {ab + b + 1} \right)\).
\( \Rightarrow \dfrac{1}{{{a^2} + 2{b^2} + 3}} \le \dfrac{1}{{2\left( {ab + b + 1} \right)}}\).
CMTT ta có:
\(\dfrac{1}{{{b^2} + 2{c^2} + 3}} \le \dfrac{1}{{2\left( {bc + c + 1} \right)}};\,\,\dfrac{1}{{{c^2} + 2{a^2} + 3}} \le \dfrac{1}{{2\left( {ca + a + 1} \right)}}\).
Khi đó ta có:
\(\begin{array}{l}\,\,\,\,\dfrac{1}{{{a^2} + 2{b^2} + 3}} + \dfrac{1}{{{b^2} + 2{c^2} + 3}} + \dfrac{1}{{{c^2} + 2{a^2} + 3}}\\ \le \dfrac{1}{2}\left( {\dfrac{1}{{ab + b + 1}} + \dfrac{1}{{bc + c + 1}} + \dfrac{1}{{ca + a + 1}}} \right)\end{array}\)
Ta có:
\(\begin{array}{l}\,\,\,\,\dfrac{1}{{ab + b + 1}} + \dfrac{1}{{bc + c + 1}} + \dfrac{1}{{ca + a + 1}}\\ = \dfrac{1}{{ab + b + 1}} + \dfrac{{ab}}{{a{b^2}c + abc + ab}} + \dfrac{b}{{bca + ab + b}}\\ = \dfrac{1}{{ab + b + 1}} + \dfrac{{ab}}{{c + 1 + ab}} + \dfrac{b}{{1 + ab + b}}\\ = \dfrac{{ab + b + 1}}{{ab + b + 1}} = 1\end{array}\)
Vậy \(\dfrac{1}{{{a^2} + 2{b^2} + 3}} + \dfrac{1}{{{b^2} + 2{c^2} + 3}} + \dfrac{1}{{{c^2} + 2{a^2} + 3}} \le \dfrac{1}{2}\). Dấu “=” xảy ra \( \Leftrightarrow a = b = c = 1\).