Đề thi vào 10 môn Toán Huế năm 2019
Tải vềCâu 1 (1,5 điểm) a) Tìm giá trị của
Đề bài
Câu 1 (1,5 điểm)
a) Tìm giá trị của \(x\) sao cho biểu thức \(A = x - 1\) có giá trị dương.
b) Đưa thừa số ra ngoài dấu căn, tính giá trị biểu thức \(B = 2\sqrt {{2^2}.5} - 3\sqrt {{3^2}.5} + 4\sqrt {{4^2}.5} .\)
c) Rút gọn biểu thức: \(C = \left( {\dfrac{{1 - a\sqrt a }}{{1 - \sqrt a }} + \sqrt a } \right){\left( {\dfrac{{1 - \sqrt a }}{{1 - a}}} \right)^2}\) với \(a \ge 0,\,\,a \ne 1.\)
Câu 2 (1,5 điểm)
a) Không sử dụng máy tính cầm tay, giải hệ phương trình: \(\left\{ \begin{array}{l}4x - y = 7\\x + 3y = 5\end{array} \right..\)
b) Cho đường thẳng \(d:\,\,y = ax + b.\) Tìm giá trị của \(a,\,\,b\) sao cho đường thẳng \(d\) đi qua điểm \(A\left( {0; - 1} \right)\) và song song với đường thẳng \(\Delta :\,\,y = x + 2019.\)
Câu 3 (1 điểm)
Hưởng ứng Ngày Chủ nhật xanh do UBNB tỉnh phát động với chủ đề: “Hãy hành động để Thừa Thiên Huế thêm Xanh, Sạch, Sáng”, một trường THCS đã cử học sinh của hai lớp 9A và 9B cùng tham gia làm tổng vệ sinh một con đường, sau \(\dfrac{{35}}{{12}}\) giờ thì làm xong công việc. Nếu làm riêng từng lớp thì thời gian học sinh lớp 9A làm xong công việc ít hơn thời gian học sinh lớp 9B là 2 giờ. Hỏi nếu mỗi lớp làm riêng thì sau bao nhiêu giờ sẽ làm xong công việc?
Câu 4 (2 điểm) Cho phương trình \({x^2} + 2\left( {m - 2} \right)x + {m^2} - 4m = 0\,\,\,\,\left( 1 \right)\) (với \(x\) là ẩn số)
a) Giải phương trình \(\left( 1 \right)\) khi \(m = 1.\)
b) Chứng minh rằng phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt với mọi giá trị của \(m.\)
c) Tìm các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn điều kiện \(\dfrac{3}{{{x_1}}} + {x_2} = \dfrac{3}{{{x_2}}} + {x_1}.\)
Câu 5 (3 điểm)
Cho đường tròn tâm \(O\) đường kính \(AB.\) Trên đường tròn \(\left( O \right)\) lấy điểm \(C\) không trùng \(B\) sao cho \(AC > BC.\) Các tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A\) và tại\(C\) cắt nhau tại \(D.\) Gọi \(H\) là hình chiếu vuông góc của \(C\) trên \(AB,\,\,\,E\) là giao điểm của hai đường thẳng \(OD\) và \(AC.\)
a) Chứng minh \(OECH\) là tứ giác nội tiếp.
b) Gọi \(F\) là giao điểm của hai đường thẳng \(CD\) và \(AB.\) Chứng minh \(2\angle BCF + \angle CFB = {90^0}.\)
c) Gọi \(M\) là giao điểm của hai đường thẳng \(BD\) và \(CH.\) Chứng minh hai đường thẳng \(EM\) và \(AB\) song song với nhau.
Câu 6 (1 điểm)
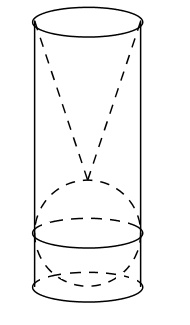
Một chiếc cốc thủy tinh có dạng hình trụ chứa đầy nước, có chiều cao bằng 6cm, bán kính đáy bằng 1cm. Người ta thả từ từ lần lượt vào cốc nước một viên bi bình cầu và một vật có dạng hình nón đều bằng thủy tinh (vừa khít như hình vẽ) thì thấy nước trong chiếc cốc tràn ra ngoài. Tính thể tích của lượng nước còn lại trong chiếc cốc (biết rằng đường kính của viên bi, đường kính của đáy hình hình nón và đường kính của đáy cốc nước xem như bằng nhau; bỏ qua bề dày của lớp vở thủy tinh).
Lời giải chi tiết
Câu 1 (1,5 điểm)
Phương pháp:
a) Giải phương bất phương trình \(A > 0\) để tìm \(x.\)
b) Sử dụng công thức \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\)
c) Sử dụng công thức hằng đẳng thức, rút gọn từng biểu thức.
Cách giải:
a) Tìm giá trị của \(x\) sao cho biểu thức \(A = x - 1\) có giá trị dương.
Ta có: \(A > 0 \Leftrightarrow x - 1 > 0 \Leftrightarrow x > 1.\)
Vậy \(x > 1\) thì \(A\) có giá trị dương.
b) Đưa thừa số ra ngoài dấu căn, tính giá trị biểu thức \(B = 2\sqrt {{2^2}.5} - 3\sqrt {{3^2}.5} + 4\sqrt {{4^2}.5} .\)
\(\begin{array}{l}B = 2\sqrt {{2^2}.5} - 3\sqrt {{3^2}.5} + 4\sqrt {{4^2}.5} \\ = 2.2\sqrt 5 - 3.3\sqrt 5 + 4.4\sqrt 5 \\ = 4\sqrt 5 - 9\sqrt 5 + 16\sqrt 5 = 11\sqrt 5 .\end{array}\)
c) Rút gọn biểu thức: \(C = \left( {\dfrac{{1 - a\sqrt a }}{{1 - \sqrt a }} + \sqrt a } \right){\left( {\dfrac{{1 - \sqrt a }}{{1 - a}}} \right)^2}\) với \(a \ge 0,\,\,a \ne 1.\)
Điều kiện \(a \ge 0,\,\,a \ne 1.\)
\(\begin{array}{l}C = \left( {\dfrac{{1 - a\sqrt a }}{{1 - \sqrt a }} + \sqrt a } \right){\left( {\dfrac{{1 - \sqrt a }}{{1 - a}}} \right)^2}\\ = \left[ {\dfrac{{\left( {1 - \sqrt a } \right)\left( {1 + \sqrt a + a} \right)}}{{1 - \sqrt a }} + \sqrt a } \right].{\left[ {\dfrac{{1 - \sqrt a }}{{\left( {1 - \sqrt a } \right)\left( {1 + \sqrt a } \right)}}} \right]^2}\\ = \left( {1 + \sqrt a + a + \sqrt a } \right).{\left( {\dfrac{1}{{1 + \sqrt a }}} \right)^2}\\ = \left( {1 + 2\sqrt a + a} \right).{\left( {\dfrac{1}{{1 + \sqrt a }}} \right)^2}\\ = {\left( {1 + \sqrt a } \right)^2}.{\left( {\dfrac{1}{{1 + \sqrt a }}} \right)^2} = 1.\end{array}\)
Câu 2 (1,5 điểm)
Phương pháp:
a) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số.
b) Hai đường thẳng \({d_1}:\,\,y = {a_1}x + {b_1},\,\,{d_2}:\,\,y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)
Cách giải:
a) Không sử dụng máy tính cầm tay, giải hệ phương trình: \(\left\{ \begin{array}{l}4x - y = 7\\x + 3y = 5\end{array} \right..\)
\(\left\{ \begin{array}{l}4x - y = 7\\x + 3y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}12x - 3y = 21\\x + 3y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}13x = 26\\y = 4x - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 4.2 - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..\)
Vậy hệ phương trình có nghiệm duy nhất:\(\left( {x;\,\,y} \right) = \left( {2;\,1} \right).\)
b) Cho đường thẳng \(d:\,\,y = ax + b.\) Tìm giá trị của \(a,\,\,b\) sao cho đường thẳng \(d\) đi qua điểm \(A\left( {0; - 1} \right)\) và song song với đường thẳng \(\Delta :\,\,y = x + 2019.\)
Ta có: \(d//\Delta \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b \ne 2019\end{array} \right. \Rightarrow d:\,\,y = x + b,\left( {b \ne 2019} \right).\)
Đường thẳng \(d:\,\,y = x + b\) đi qua điểm \(A\left( {0; - 1} \right)\) nên thay tọa độ điểm \(A\) vào phương trình đường thẳng \(d\) ta được: \( - 1 = 0 + b \Leftrightarrow b = - 1\,\,\left( {tm} \right)\)
Vậy \(a = 1;\,\,b = - 1.\)
Câu 3 (1 điểm)
Phương pháp:
Gọi thời gian lớp 9A làm một mình xong công việc là \(x\) (giờ) \(\left( {x > \dfrac{{35}}{{12}}} \right).\)
Gọi thời gian lớp 9B làm một mình xong công việc là \(y\) (giờ) \(\left( {y > 2} \right).\)
Biểu diễn các đại lượng chưa biết theo \(x,\,y\) rồi lập hệ phương trình.
Giải hệ phương trình tìm các ẩn \(x,\,\,y,\) đối chiếu với điều kiện rồi kết luận.
Cách giải:
Gọi thời gian lớp 9A làm một mình xong công việc là \(x\) (giờ) \(\left( {x > \dfrac{{35}}{{12}}} \right).\)
Gọi thời gian lớp 9B làm một mình xong công việc là \(y\) (giờ) \(\left( {y > 2} \right).\)
\( \Rightarrow \) Mỗi giờ lớp 9A làm được phần công việc là: \(\dfrac{1}{x}\) (công việc).
Mỗi giờ lớp 9B làm được phần công việc là: \(\dfrac{1}{y}\) (công việc).
Mỗi giờ thì cả hai lớp 9A và 9B làm được phần công việc là: \(1:\dfrac{{35}}{{12}} = \dfrac{{12}}{{35}}\) (công việc).
Theo đề bài ta có hai lớp cùng làm chung công việc trong \(\dfrac{{35}}{{12}}\) giờ thì xong công việc nên ta có phương trình:
\(\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{{12}}{{35}}\,\,\,\,\left( 1 \right)\)
Nếu làm riêng từng lớp thì thời gian học sinh lớp 9A làm xong công việc ít hơn thời gian học sinh lớp 9B là 2 giờ nên ta có phương trình: \(y = x + 2\,\,\,\left( 2 \right)\)
Thế phương trình (2) vào phương trình (1) ta được:
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow \dfrac{1}{x} + \dfrac{1}{{x + 2}} = \dfrac{{12}}{{35}} \Leftrightarrow 35\left( {x + 2} \right) + 35x = 12x\left( {x + 2} \right)\\ \Leftrightarrow 35x + 70 + 35x = 12{x^2} + 24x\\ \Leftrightarrow 12{x^2} - 46x - 70 = 0\\ \Leftrightarrow 12{x^2} - 60x + 14x - 70 = 0\\ \Leftrightarrow 12x\left( {x - 5} \right) + 14\left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 5} \right)\left( {12x + 14} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\12x + 14 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\,\,\,\left( {tm} \right)\\x = - \dfrac{7}{6}\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy nếu làm việc một mình thì lớp 9A làm xong công việc sau \(5\) giờ, lớp 9B làm xong công việc trong \(5 + 2 = 7\) giờ.
Câu 4 (2 điểm)
Phương pháp:
a) Thay \(m = 1\) vào phương trình \(\left( 1 \right)\) rồi giải phương trình bậc hai.
b) Phương trình đã cho có hai nghiệm phân biệt với mọi \(m \Leftrightarrow \Delta ' > 0\,\,\forall m.\)
c) Áp dụng định lí Vi-et và giả thiết bài toán để tìm \(m.\)
Cách giải:
a) Giải phương trình \(\left( 1 \right)\) khi \(m = 1.\)
Thay \(m = 1\) vào phương trình \(\left( 1 \right)\) ta được phương trình
\(\begin{array}{l} \Leftrightarrow {x^2} - 2x - 3 = 0 \Leftrightarrow {x^2} - 3x + x - 3 = 0\\ \Leftrightarrow x\left( {x - 3} \right) + \left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 1\end{array} \right..\end{array}\)
Vậy với \(m = 1\) thì tập nghiệm của phương trình là:\(S = \left\{ { - 1;\,\,3} \right\}.\)
b) Chứng minh rằng phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt với mọi giá trị của \(m.\)
\({x^2} + 2\left( {m - 2} \right)x + {m^2} - 4m = 0\,\,\,\,\left( 1 \right)\)
Có \(\Delta ' = {\left( {m - 2} \right)^2} - {m^2} + 4m = {m^2} - 4m + 4 - {m^2} + 4m = 4 > 0\,\,\,\forall m\)
Vậy phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt với mọi giá trị của \(m.\)
c) Tìm các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn điều kiện \(\dfrac{3}{{{x_1}}} + {x_2} = \dfrac{3}{{{x_2}}} + {x_1}.\)
Phương trình \(\left( 1 \right)\) luôn có hai nghiệm \({x_1},\,\,{x_2}\) với mọi giá trị của \(m.\)
Áp dụng hệ thức Vi-ét ta có:\(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\left( {m - 2} \right) = - 2m + 4\\{x_1}{x_2} = {m^2} - 4m\end{array} \right..\)
Theo bài ra ta có: \(\dfrac{3}{{{x_1}}} + {x_2} = \dfrac{3}{{{x_2}}} + {x_1}\)
\(\begin{array}{l} \Leftrightarrow \dfrac{3}{{{x_1}}} - \dfrac{3}{{{x_2}}} - {x_1} + {x_2} = 0\,\,\,\,\,\left( {{x_1}{x_2} \ne 0 \Leftrightarrow {m^2} - 4m \ne 0 \Leftrightarrow m \ne 0,m \ne 4} \right)\\ \Leftrightarrow 3\left( {\dfrac{1}{{{x_1}}} - \dfrac{1}{{{x_2}}}} \right) + \left( {{x_2} - {x_1}} \right) = 0\\ \Leftrightarrow \dfrac{{3\left( {{x_2} - {x_1}} \right)}}{{{x_1}{x_2}}} + \left( {{x_2} - {x_1}} \right) = 0\\ \Leftrightarrow \left( {{x_2} - {x_1}} \right)\left( {\dfrac{3}{{{x_1}{x_2}}} + 1} \right) = 0\\ \Leftrightarrow \dfrac{3}{{{x_1}{x_2}}} + 1 = 0\,\,\,\left( {do\,\,\,{x_1} \ne {x_2} \Rightarrow {x_2} - {x_1} \ne 0} \right)\\ \Leftrightarrow \dfrac{3}{{{m^2} - 4m}} + 1 = 0\\ \Leftrightarrow {m^2} - 4m + 3 = 0\\ \Leftrightarrow {m^2} - 3m - m + 3 = 0\\ \Leftrightarrow m\left( {m - 3} \right) - \left( {m - 3} \right) = 0\\ \Leftrightarrow \left( {m - 3} \right)\left( {m - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 3 = 0\\m - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\,\left( {tm} \right)\\m = 1\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(m = 1;m = 3\) là các giá trị thỏa mãn bài toán.
Câu 5 (3 điểm)
Phương pháp:
a) Sử dụng dấu hiệu nhận biết để chứng minh tứ giác nội tiếp.
b) Trong một đường tròn, góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung thì bằng nhau.
c) Sử dụng tính chất đường trung bình để chứng minh song song.
Cách giải:
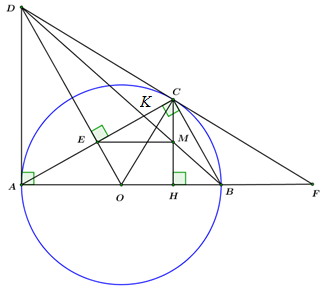
a) Chứng minh \(OECH\) là tứ giác nội tiếp.
Ta có: \(CH \bot AB = \left\{ H \right\} \Rightarrow \angle CHO = {90^0}.\)
Xét đường tròn \(\left( O \right)\) ta có:
\(AD = CD\) (tính chất hai tiếp tuyến cắt nhau)
\(OA = OC\,\,\left( { = R} \right)\)
\( \Rightarrow OD\) là đường trung trực của \(AC.\)
\( \Rightarrow OD \bot AC = \left\{ E \right\} \Rightarrow \angle CEO = {90^0}\)
Xét tứ giác \(OECH\) ta có: \(\angle CEO + \angle CHO = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow OECH\) là tứ giác nội tiếp. (Tứ giác có tổng hai góc đối diện bằng \({180^0}\))
b) Gọi \(F\) là giao điểm của hai đường thẳng \(CD\) và \(AB.\) Chứng minh \(2\angle BCF + \angle CFB = {90^0}.\)
Xét đường tròn \(\left( O \right)\) ta có:
\(\angle BAC = \angle BCF\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(BC\)) (1)
Xét \(\Delta CBA\) và \(\Delta HBC\) ta có:
\( \Rightarrow \angle BAC = \angle HCB\,\,\,\,\left( 2 \right)\) (hai góc tương ứng).
Từ (1) và (2) suy ra: \(\angle BCF = \angle HCB\)
Mặt khác ta có: \(\Delta CHF\) vuông tại H (do \(CH \bot AB\) ) khi đó ta có:
\(\angle HCF + \angle CFH = {90^0} \Leftrightarrow 2\angle BCF + \angle CFB = {90^0}\,\,\,\left( {dpcm} \right).\)
c) Gọi \(M\) là giao điểm của hai đường thẳng \(BD\) và \(CH.\) Chứng minh hai đường thẳng \(EM\) và \(AB\) song song với nhau.
Gọi \(K\) là giao điểm của \(DB\) và \(AC.\)
Xét đường tròn \(\left( O \right)\) ta có: \(\angle ABC = \angle ACD\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AC\))
Ta có: \(\Delta ACH\) vuông tại \(H \Rightarrow \angle ACH + \angle CAH = {90^0}.\)
\(\Delta ABC\) vuông tại \(C \Rightarrow \angle CAB + \angle CBA = {90^0}\)
\( \Rightarrow \angle ACH = \angle ABC\) (cùng phụ với \(\angle CAH\))
\( \Rightarrow \angle CAH = \angle DCA = \angle DCK\,\,\left( { = \angle CBA} \right)\)
\( \Rightarrow CK\) là phân giác trong của \(\angle DCM\) trong \(\Delta CDM.\)
Lại có: \(\angle BCF = \angle BCH = \angle BCM\,\,\,\left( {cm\,\,b} \right)\)
\( \Rightarrow BC\) là phân giác ngoài của \(\angle DCM\) trong \(\Delta DCM.\)
Áp dụng tính chất tia phân giác của tam giác trong \(\Delta DCM\) ta có: \(\dfrac{{KM}}{{KD}} = \dfrac{{BM}}{{BD}} = \dfrac{{CM}}{{CD}}.\)
Lại có: \(AC = AD\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow \dfrac{{KM}}{{KD}} = \dfrac{{BM}}{{BD}} = \dfrac{{CM}}{{AD}}.\)
Ta có: \(CH//AD\,\,\left( { \bot AB} \right)\)
\( \Rightarrow \dfrac{{HM}}{{AD}} = \dfrac{{BM}}{{BD}}\) (định lý Ta-let)
\(\begin{array}{l} \Rightarrow \dfrac{{HM}}{{AD}} = \dfrac{{CM}}{{AD}} = \dfrac{{BM}}{{BD}}\\ \Rightarrow HM = CM\end{array}\)
\( \Rightarrow M\) là trung điểm của \(CH.\)
Mà \(E\) là trung điểm của \(CA\,\,\) (\(OD\) là trung trực của \(AC\))
\( \Rightarrow ME\) là đường trung bình của \(\Delta CAH.\) (định nghĩa đường trung bình)
\( \Rightarrow ME//AH\,\,\,hay\,\,\,ME//AB.\,\,\,\,\left( {dpcm} \right).\)
Câu 6 (1,0 điểm)
Phương pháp:
Áp dụng các công thức tính thể tích của hình trụ, hình nón, hình cầu:
\({V_{tru}} = \pi {r^2}h;\,\,{V_{non}} = \dfrac{1}{3}\pi {r^2}h;\,\,{V_{cau}} = \dfrac{4}{3}\pi {r^3}\)
Cách giải:
+) Ta có hình trụ có : \({h_{tru}} = 6\,cm,{r_{tru}} = 1\,cm\)
\({V_{tru}} = \pi {r_{tru}}^2{h_{tru}} = \pi {.1^2}.6 = 6\pi \,\left( {c{m^3}} \right)\)
+) Ta có: \({r_{cau}} = {r_{tru}} = 1\left( {cm} \right)\)
\({V_{cau}} = \dfrac{4}{3}\pi r_{cau}^3 = \dfrac{4}{3}\pi {.1^3} = \dfrac{4}{3}\pi \left( {c{m^3}} \right)\)
Theo hình vẽ ta có: \({h_{non}} = {h_{tru}} - 2{r_{cau}} = 6 - 2 = 4\left( {cm} \right)\)
\({V_{non}} = \dfrac{1}{3}\pi {r^2}_{non}.{h_{non}} = \dfrac{1}{3}.\pi {.1^2}.4 = \dfrac{4}{3}\pi \left( {c{m^3}} \right)\)
Khi đó ta có thể tích của lượng nước còn lại trong chiếc cốc là:
\(V = {V_{tru}} - {V_{non}} - {V_{cau}} = 6\pi - \dfrac{4}{3}\pi - \dfrac{4}{3}\pi = \dfrac{{10}}{3}\pi \,\,\left( {c{m^3}} \right)\)