Đề thi vào 10 môn Toán Quảng Bình 2023 có đáp án và lời giải chi tiết — Không quảng cáo

Đề bài

Câu 1: Cho biểu thức $A = \frac{1}{{\sqrt a {\rm{ \;}} + 3}} + \frac{6}{{a - 9}}$ với $a \ge 0$ và $a \ne 9$.

1. Rút gọn biểu thức $A$.

2. Tìm tất cả các giá trị của $a$ để $A = \frac{1}{2}$.

Câu 2: 1. Giải phương trình ${x^2} + 5x - 6 = 0$.

2. Cho phương trình ${x^2} + 5x + m - 3 = 0$ ( $m$ là tham số).

a. Tìm tất cả các giá trị của $m$ để phương trình có hai nghiệm.

b. Trong trường hợp phương trình có hai nghiệm ${x_1},{x_2}$, tìm tất cả các giá trị của m để ${x_1},{x_2}$ thỏa mãn hệ thức $2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2$.

Câu 3: Với $x \in \mathbb{R}$, tìm giá trị nhỏ nhất của biểu thức $P = 4{x^2} - 2|2x - 3| - 12x + 2033$.

Câu 4: Cho nửa đường tròn tâm O đường kính BC và điểm 4 thuộc nửa đường tròn đó, (A khác B và C). Lấy điểm E thuộc cung AB (E khác A và B) sao cho BE < AC, gọi M là giao điểm của AB và CE. Kẻ MH vuông góc với BC tại H.

1. Chứng minh tứ giác ACHM nội tiếp.

2. Chứng minh $\Delta$BAE đồng dạng với $\Delta$HAM .

3. Gọi K là giao điểm của OE và HA. Chứng minh KE.KO = KA.KH.

----- HẾT -----

Lời giải chi tiết

Câu 1 (VD):

Phương pháp:

1.Sử dụng tính chất căn bậc hai.

2. Giải phương trình với A vừa rút gọn.

Cách giải:

1. Rút gọn biểu thức $A$ .

Với $a \ge 0$ và $a \ne 9$ ta có:

$\begin{array}{l}A = \frac{1}{{\sqrt a  + 3}} + \frac{6}{{a - 9}}\\\,\,\,\, = \frac{1}{{\sqrt a  + 3}} + \frac{6}{{\left( {\sqrt a  + 3} \right)\left( {\sqrt a  - 3} \right)}}\\\,\,\, = \frac{{\sqrt a  - 3}}{{\left( {\sqrt a  + 3} \right)\left( {\sqrt a  - 3} \right)}} + \frac{6}{{\left( {\sqrt a  + 3} \right)\left( {\sqrt a  - 3} \right)}}\\\,\,\, = \frac{{\sqrt a  + 3}}{{\left( {\sqrt a  + 3} \right)\left( {\sqrt a  - 3} \right)}}\\\,\,\, = \frac{1}{{\sqrt a  - 3}}\end{array}$

Vậy $A = \frac{1}{{\sqrt a  - 3}}.$

2. Tìm tất cả các giá trị của $a$ để $A = \frac{1}{2}$ .

Với $a \ge 0$ và $a \ne 9$ ta có: $A = \frac{1}{{\sqrt a  - 3}}.$

Vậy với $a = 5$ thì $A = \frac{1}{2}$.

Câu 2 (VD):

Phương pháp:

1. Tính $\Delta {\rm{ \;}} = {b^2} - 4.a.c$

- $\Delta {\rm{ \;}} = 0$ thì phương trình có nghiệm kép ${x_1} = {x_2} = \frac{{ - b}}{{2a}}$

- $\Delta {\rm{ \;}} < 0$ thì phương trình vô nghiệm

-  $\Delta {\rm{ \;}} > 0$thì phương trình có hai nghiệm phân biệt:

${x_1} = \frac{{ - b + \sqrt \Delta  {\rm{ \;}}}}{{2.a}}$

${x_2} = \frac{{ - b - \sqrt \Delta  {\rm{ \;}}}}{{2.a}}$

2. Sử dụng vi ét.

Cách giải:

1. Giải phương trình ${x^2} + 5x - 6 = 0$ .

Xét phương trình ${x^2} + 5x - 6 = 0$ có $a + b + c = 1 + 5 - 6 = 0$ phương trình có hai nghiệm phân biệt $\left[ \begin{array}{l}{x_1} = 1\\{x_2} =  - 6\end{array} \right.$

Vậy phương trình có hai nghiệm phân biệt $\left[ \begin{array}{l}{x_1} = 1\\{x_2} =  - 6\end{array} \right.$.

2. Cho phương trình ${x^2} + 5x + m - 3 = 0$ ( $m$ là tham số).

a. Tìm tất cả các giá trị của $m$ để phương trình có hai nghiệm.

Xét phương trình ${x^2} + 5x + m - 3 = 0$ có $\Delta  = {5^2} - 4.1.\left( {m - 3} \right) = 25 - 4m + 12 = 37 - 4m$

Để phương trình có hai nghiệm thì $\Delta  \ge 0 \Leftrightarrow 37 - 4m \ge 0 \Leftrightarrow  - 4m \ge  - 37 \Leftrightarrow m \le \frac{{37}}{4}$.

Vậy phương trình có hai nghiệm khi $m \le \frac{{37}}{4}$.

b. Trong trường hợp phương trình có hai nghiệm ${x_1},{x_2}$ , tìm tất cả các giá trị của $m$ để ${x_1},{x_2}$ thỏa mãn hệ thức $2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2$ .

Theo a, phương trình có hai nghiệm khi $m \le \frac{{37}}{4}$.

Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình.

Áp dụng định lí Vi – ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} =  - 5\\{x_1}.{x_2} = m - 3\end{array} \right.$

Để $2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2$

$\begin{array}{l}2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2\\ \Leftrightarrow 2\left( {m - 3} \right) - \left( { - 5} \right) = 2\\ \Leftrightarrow 2m = 3\\ \Leftrightarrow m = \frac{3}{2}\left( {tm} \right).\end{array}$

Vậy với $m = \frac{3}{2}$ thì phương trình có hai nghiệm ${x_1},{x_2}$, mãn hệ thức $2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 2$.

Câu 3 (NB):

Cách giải:

Ta có:

$\begin{array}{l}P = 4{x^2} - 2|2x - 3| - 12x + 2033\\\,\,\,\,\, = \left( {4{x^2} - 12x + 9} \right) - 2|2x - 3| + 2024\\\,\,\,\,\, = {\left( {2x - 3} \right)^2} - 2|2x - 3| + 2024\end{array}$

Đặt $t = |2x - 3| \ge 0$

Khi đó ta có: $P = {t^2} - 2t + 2024 = {(t - 1)^2} + 2023$

Vì $t \ge 0 \Rightarrow t - 1 \ge  - 1 \Rightarrow {(t - 1)^2} \ge 0$ nên $P \ge 0 + 2023 = 2023$

Dấu bằng xảy ra khi và chỉ khi $t - 1 = 0 \Leftrightarrow t = 1$

Suy ra: $|2x - 3| = 1 \Leftrightarrow \left[ \begin{array}{l}2x - 3 = 1\\2x - 3 =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 4\\2x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.$

Vậy giá trị nhỏ nhất của P là $2023$ khi $x = 1$ hoặc $x = 2.$

Câu 4 (NB):

Cách giải:

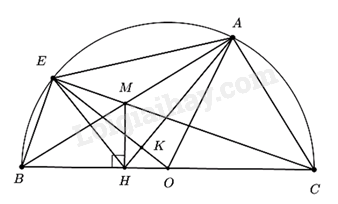
1. Chứng minh tứ giác ACHM nội tiếp.

Ta có $\angle BAC = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

Mà $\angle MHC = {90^0}\left( {MH \bot BC} \right)$

$\Rightarrow \angle MHC + \angle MAC = {90^0} + {90^0} = {180^0}$

Mà 2 góc này ở vị trí đối diện nên tứ giác MHCA nội tiếp (dhnb) (đpcm)

2. Chứng minh $\Delta$ BAE đồng dạng với $\Delta$ HAM .

Do AMHC nội tiếp (cmt) nên $\angle MAH = \angle MCH$ (cùng chắn cung MH)

Và $\angle MHA = \angle MCA$ (cùng chắn cung AM)

Mà $\angle MCH = \angle ECB = \angle EAB$ (cùng chắn cung EB)  và $\angle ACE = \angle EBA$ (cùng chắn cung AE)

$\Rightarrow \angle MAH = \angle EAB\left( { = \angle ECB} \right)$ và $\angle MHA = \angle EBA\left( { = \angle ECA} \right)$

Xét $\Delta MHA$ và $\Delta EBA$ có:

$\angle MAH = \angle EAB$ (cmt)

$\angle MHA = \angle EBA$ (cmt)

$\Rightarrow \Delta MAH\backsim \Delta EAB\left( g.g \right)$ (đpcm)

3. Gọi K là giao điểm của OE và HA. Chứng minh KE.KO = KA.KH.

Do MHCA nội tiếp nên $\angle AHC = \angle AMC$ (cùng chắn cung AC)

Mà $\angle AMC = \frac{1}{2}\left( {sdcAC + sdcEB} \right) = \frac{1}{2}\left( {{{180}^0} - sdcAE} \right) = \frac{1}{2}\left( {{{180}^0} - \angle EOA} \right) = \frac{1}{2}\left( {\angle AEO + \angle EAO} \right)$

Mà $\Delta OEA$ cân do OA = OE nên $\angle OEA = \angle OAE$

$\Rightarrow \angle AMC = \frac{1}{2}.2.\angle OEA = \angle OEA$

$\Rightarrow \angle AHO = \angle AEO\left( { = \angle AMC} \right)$

Xét tứ giác OHEA có $\angle AHO = \angle AEO$

Mà H, E là 2 đỉnh kề nhau cùng nhìn OA dưới 2 góc bằng nhau nên OHEA nội tiếp

$\Rightarrow \angle KAO = \angle KEH$ (cùng chắn cung OH) và $\angle KOA = \angle KHE$ (cùng chắn cung AE)

Xét $\Delta KOA$ và $\Delta KHE$ có:

$\angle KAO = \angle KEH\left( {cmt} \right)$

$\angle KOA = \angle KHE\left( {cmt} \right)$

$\Rightarrow \Delta KOA\backsim \Delta KHE\left( g.g \right)\Rightarrow \frac{KO}{KH}=\frac{KA}{KE}\Rightarrow KO.KE=KH.KA$  (đpcm)