Đề thi vào 10 môn Toán Sơn La năm 2020
Tải vềCâu 1: Cho biểu thức:
Đề bài
Câu 1:
Cho biểu thức: \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x + 2}} - \dfrac{1}{{\sqrt x - 2}}\)
a) Tìm điều kiện để biểu thức \(A\) xác định.
b) Rút gọn biểu thức \(A.\)
Câu 2:
Trên cùng hệ trục tọa độ vẽ hai đồ thị hàm số \(y = x + 2\) và \(y = {x^2}\). Tìm tọa độ giao điểm của hai đồ thị đó.
Câu 3:
Giải các phương trình sau:
a) \(\dfrac{x}{2} + 2020 = x + \dfrac{{2035}}{2}\) b) \({x^2} - 2\sqrt 2 x - 6 = 0\) c) \({x^2} + \dfrac{{9{x^2}}}{{{{\left( {x + 3} \right)}^2}}} = 7\,\,\)
Câu 4:
Cho phương trình \({x^2} + 2\left( {m - 3} \right)x + m - 1 = 0\) với \(m\) là tham số. Tìm \(m\) để phương trình có đúng hai nghiệm dương.
Câu 5:
Một mảnh vườn hình chữ nhật có diện tích \(480{m^2}\). Nếu tăng chiều dài lên 8m và giảm chiều rộng đi 2m thì diện tích không đổi. Hãy tính chu vi của mảnh vườn đó.
Câu 6:
Từ một điểm \(A\) bên ngoài đường tròn tâm \(O\) vẽ các tiếp tuyến \(AB,\,\,AC\) (\(B\) và \(C\) là các tiếp điểm). Gọi \(H\) là giao điểm của \(OA\) và \(BC\).
a) Chứng minh tứ giác \(ABOC\) nội tiếp được đường tròn.
b) Tính diện tích tam giác \(ABC\) trong trường hợp bán kính đường tròn \(\left( O \right)\) bằng \(R\) và \(AO = 3R\).
c) Dây cung \(EF\) thay đổi nhưng luôn đi qua \(H\). Chứng minh \(AO\) là tia phân giác góc \(\angle EAF\).
Lời giải
Câu 1 (1,5 điểm)
Cách giải:
Cho biểu thức: \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x + 2}} - \dfrac{1}{{\sqrt x - 2}}\)
a) Tìm điều kiện để biểu thức \(A\) xác định.
Điều kiện: \(\left\{ \begin{array}{l}x \ge 0\\x - 4 \ne 0\\\sqrt x - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ne 4\\\sqrt x \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ne 4\end{array} \right..\)
Vậy biểu thức \(A\) xác định khi \(x \ge 0,\,\,x \ne 4.\)
b) Rút gọn biểu thức \(A.\)
Điều kiện:\(x \ge 0,\,\,x \ne 4.\)
\(\begin{array}{l}A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x + 2}} - \dfrac{1}{{\sqrt x - 2}}\\\,\,\,\, = \dfrac{x}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \dfrac{1}{{\sqrt x + 2}} - \dfrac{1}{{\sqrt x - 2}}\\\,\,\, = \dfrac{{x + \sqrt x - 2 - \sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\\,\,\, = \dfrac{{x - 4}}{{x - 4}} = 1.\end{array}\)
Vậy \(A = 1\) khi \(x \ge 0,\,\,x \ne 4.\)
Câu 2 (1,0 điểm)
Cách giải:
Trên cùng hệ trục tọa độ vẽ hai đồ thị hàm số \(y = x + 2\) và \(y = {x^2}\) . Tìm tọa độ giao điểm của hai đồ thị đó.
+ Vẽ đồ thị hàm số.
Vẽ đường thẳng \(y = x + 2\).
Ta có bảng giá trị sau:
|
\(x\) |
\(0\) |
\( - 2\) |
|
\(y\) |
\(2\) |
\(0\) |
\( \Rightarrow \) Đường thẳng \(y = x + 2\) là đường thẳng đi qua các điểm \(\left( {0;2} \right);\,\,\left( { - 2;0} \right)\).
Vẽ parabol \(y = {x^2}\).
Ta có bảng giá trị sau:
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y\) |
4 |
1 |
0 |
1 |
4 |
\( \Rightarrow \) Parabol \(y = {x^2}\) là đường cong đi qua các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) và nhận trục \(Oy\) là trục đối xứng.
Vẽ đồ thị hàm số:
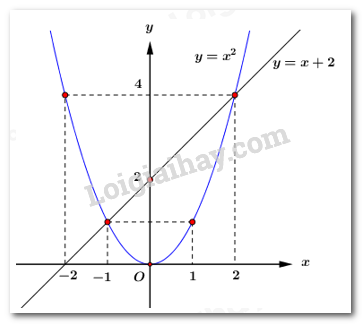
Cách 1:
Dựa vào đồ thị ta thấy hai đồ thị hàm số \(y = x + 2\) và \(y = {x^2}\) cắt nhau tại hai điểm \(\left( { - 1;1} \right)\) và \(\left( {2;4} \right)\).
Cách 2:
Xét phương trình hoành độ giao điểm:
\(\begin{array}{l}\,\,\,\,\,x + 2 = {x^2}\\ \Leftrightarrow {x^2} - x - 2 = 0\\ \Leftrightarrow {x^2} + x - 2x - 2 = 0\\ \Leftrightarrow x\left( {x + 1} \right) - 2\left( {x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\end{array}\)
Với \(x = - 1 \Rightarrow y = {\left( { - 1} \right)^2} = 1 \Rightarrow A\left( { - 1;1} \right)\).
Với \(x = 2 \Rightarrow y = {2^2} = 4 \Rightarrow B\left( {2;4} \right)\).
Vậy hai đồ thị hàm số \(y = x + 2\) và \(y = {x^2}\) cắt nhau tại 2 điểm có tọa độ là \(A\left( { - 1;1} \right)\) và \(B\left( {2;4} \right)\).
Câu 3 (2,0 điểm)
Cách giải:
Giải các phương trình sau:
a) \(\dfrac{x}{2} + 2020 = x + \dfrac{{2035}}{2}\)
\(\begin{array}{l} \Leftrightarrow x - \dfrac{x}{2} = 2020 - \dfrac{{2035}}{2}\\ \Leftrightarrow \dfrac{x}{2} = \dfrac{{2005}}{2}\\ \Leftrightarrow x = 2005.\end{array}\)
Vậy phương trình có nghiệm \(x = 2005.\)
b) \({x^2} - 2\sqrt 2 x - 6 = 0\)
Ta có: \(\Delta ' = 2 + 6 = 8 > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \sqrt 2 + \sqrt 8 = \sqrt 2 + 2\sqrt 2 = 3\sqrt 2 \\{x_2} = \sqrt 2 - \sqrt 8 = \sqrt 2 - 2\sqrt 2 = - \sqrt 2 \end{array} \right..\)
Vậy phương trình có tập nghiệm: \(S = \left\{ { - \sqrt 2 ;\,\,3\sqrt 2 } \right\}.\)
c) \({x^2} + \dfrac{{9{x^2}}}{{{{\left( {x + 3} \right)}^2}}} = 7\,\,\,\left( * \right)\)
Điều kiện: \(x + 3 \ne 0 \Leftrightarrow x \ne 3.\)
\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow {x^2} - 2.\dfrac{{3{x^2}}}{{x + 3}} + \dfrac{{9{x^2}}}{{{{\left( {x + 3} \right)}^2}}} + \dfrac{{6{x^2}}}{{x + 3}} = 7\\ \Leftrightarrow {\left( {x - \dfrac{{3x}}{{x + 3}}} \right)^2} + \dfrac{{6{x^2}}}{{x + 3}} - 7 = 0\\ \Leftrightarrow {\left( {\dfrac{{{x^2} + 3x - 3x}}{{x + 3}}} \right)^2} + \dfrac{{6{x^2}}}{{x + 3}} - 7 = 0\\ \Leftrightarrow {\left( {\dfrac{{{x^2}}}{{x + 3}}} \right)^2} + \dfrac{{6{x^2}}}{{x + 3}} - 7 = 0\,\,\,\,\left( 1 \right)\end{array}\)
Đặt \(\dfrac{{{x^2}}}{{x + 3}} = t\)
\(\begin{array}{l} \Rightarrow \left( 1 \right) \Leftrightarrow {t^2} + 6t - 7 = 0\\ \Leftrightarrow {t^2} + 7t - t - 7 = 0\\ \Leftrightarrow t\left( {t + 7} \right) - \left( {t + 7} \right) = 0\\ \Leftrightarrow \left( {t + 7} \right)\left( {t - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t + 7 = 0\\t - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - 7\\t = 1\end{array} \right.\end{array}\)
+) Với \(t = - 7\) ta có: \(\dfrac{{{x^2}}}{{x + 3}} = - 7\)
\(\begin{array}{l} \Leftrightarrow {x^2} = - 7x - 21\\ \Leftrightarrow {x^2} + 7x + 21 = 0\end{array}\)
Có \(\Delta = {7^2} - 4.21 = - 35 < 0\)
\( \Rightarrow \) Phương trình vô nghiệm.
+) Với \(t = 1\) ta có:\(\dfrac{{{x^2}}}{{x + 3}} = 1\)
\(\begin{array}{l} \Leftrightarrow {x^2} = x + 3\\ \Leftrightarrow {x^2} - x - 3 = 0\end{array}\)
Có \(\Delta = 1 + 4.3 = 13 > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{1 - \sqrt {13} }}{2}\,\,\left( {tm} \right)\\{x_2} = \dfrac{{1 + \sqrt {13} }}{2}\,\,\left( {tm} \right)\end{array} \right..\)
Vậy tập nghiệm của phương trình là:\(S = \left\{ {\dfrac{{1 - \sqrt {13} }}{2};\,\,\,\dfrac{{1 + \sqrt {13} }}{2}} \right\}.\)
Câu 4 (1,0 điểm)
Cách giải:
Cho phương trình \({x^2} + 2\left( {m - 3} \right)x + m - 1 = 0\) với \(m\) là tham số. Tìm \(m\) để phương trình có đúng hai nghiệm dương.
Để phương trình \({x^2} + 2\left( {m - 3} \right)x + m - 1 = 0\) có hai nghiệm dương thì:
\(\begin{array}{l}\left\{ \begin{array}{l}\Delta ' \ge 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 3} \right)^2} - \left( {m - 1} \right) \ge 0\\ - 2\left( {m - 3} \right) > 0\\m - 1 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 6m + 9 - m + 1 \ge 0\\m - 3 < 0\\m > 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 7m + 10 \ge 0\\m < 3\\m > 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 7m + 10 \ge 0\,\,\,\left( 1 \right)\\1 < m < 3\end{array} \right.\,\,\left( * \right)\end{array}\)
Xét bất phương trình \({m^2} - 7m + 10 \ge 0\,\,\left( 1 \right)\) ta có:
\(\begin{array}{l}\,\,\,\,\,{m^2} - 7m + 10 \ge 0\\ \Leftrightarrow {m^2} - 2m - 5m + 10 \ge 0\\ \Leftrightarrow m\left( {m - 2} \right) - 5\left( {m - 2} \right) \ge 0\\ \Leftrightarrow \left( {m - 2} \right)\left( {m - 5} \right) \ge 0\end{array}\)
TH1: \(\left\{ \begin{array}{l}m - 2 \ge 0\\m - 5 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge 2\\m \ge 5\end{array} \right. \Leftrightarrow m \ge 5\).
TH2: \(\left\{ \begin{array}{l}m - 2 \le 0\\m - 5 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 2\\m \le 5\end{array} \right. \Leftrightarrow m \le 2\).
Do đó \(\left( 1 \right) \Leftrightarrow \left[ \begin{array}{l}m \ge 5\\m \le 2\end{array} \right.\).
Khi đó hệ (*) trở thành: \(\left\{ \begin{array}{l}\left[ \begin{array}{l}m \ge 5\\m \le 2\end{array} \right.\\1 < m < 3\end{array} \right. \Rightarrow 1 < m \le 2\).
Vậy \(1 < m \le 2\).
Câu 5 (1,0 điểm)
Cách giải:
Một mảnh vườn hình chữ nhật có diện tích \(480{m^2}\) . Nếu tăng chiều dài lên 8m và giảm chiều rộng đi 2m thì diện tích không đổi. Hãy tính chu vi của mảnh vườn đó.
Gọi chiều dài và chiều rộng của mảnh vườn lần lượt là \(x,\,\,y\) (mét) (ĐK: \(x > y > 2\)).
Vì diện tích mảnh vườn là \(480{m^2}\) nên ta có phương trình \(xy = 480\,\,\left( 1 \right)\).
Nếu tăng chiều dài lên 8m thì chiều dài mới là \(x + 8\,\,\left( m \right)\).
giảm chiều rộng đi 2m thì chiều chiều rộng mới là \(y - 2\,\,\left( m \right)\).
Khi đó diện tích mảnh vườn không thy đổi nên ta có phương trình
\(\begin{array}{l}\,\,\,\,\,\left( {x + 8} \right)\left( {y - 2} \right) = 480\\ \Leftrightarrow xy - 2x + 8y - 16 = 480\\ \Leftrightarrow 480 - 2x + 8y - 16 = 480\\ \Leftrightarrow 2x - 8y = - 16\\ \Leftrightarrow x - 4y = - 8\,\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}xy = 480\\x - 4y = - 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}xy = 480\\x = 4y - 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}\left( {4y - 8} \right).y = 480\\x = 4y - 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{y^2} - 8y - 480 = 0\\x = 4y - 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{y^2} - 2y - 120 = 0\,\,\left( * \right)\\x = 4y - 8\end{array} \right.\)
Xét phương trình (*) ta có:
\(\begin{array}{l}\,\,\,\,\,\,{y^2} - 2y - 120 = 0\\ \Leftrightarrow {y^2} - 12y + 10y - 120 = 0\\ \Leftrightarrow y\left( {y - 12} \right) + 10\left( {y - 12} \right) = 0\\ \Leftrightarrow \left( {y - 12} \right)\left( {y + 10} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}y - 12 = 0\\y + 10 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = 12\,\,\,\,\,\,\,\left( {tm} \right)\\y = - 10\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Với \(y = 12\) \( \Rightarrow x = 4.12 - 8 = 40\).
Vậy chu vi của mảnh vườn đó là \(C = 2\left( {x + y} \right) = 2\left( {40 + 12} \right) = 104\,\,\left( m \right)\).
Câu 6 (1,0 điểm)
Cách giải:
Từ một điểm \(A\) bên ngoài đường tròn tâm \(O\) vẽ các tiếp tuyến \(AB,\,\,AC\) ( \(B\) và \(C\) là các tiếp điểm). Gọi \(H\) là giao điểm của \(OA\) và \(BC\) .

a) Chứng minh tứ giác \(ABOC\) nội tiếp được đường tròn.
Ta có: \(AB,\,\,AC\) là các tiếp tuyến của đường tròn \(\left( O \right)\)
\( \Rightarrow \left\{ \begin{array}{l}AB \bot OB\\AC \bot OC\end{array} \right. \Rightarrow \angle ABO = \angle ACO = {90^0}\)
Xét tứ giác \(ABOC\) ta có:
\(\angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow \angle ABOC\) là tứ giác nội tiếp (dhnb). (đpcm)
b) Tính diện tích tam giác \(ABC\) trong trường hợp bán kính đường tròn \(\left( O \right)\) bằng \(R\) và \(AO = 3R\) .
Ta có:\(OB = OC = R\)
\( \Rightarrow O\) thuộc đường trung trực của \(BC.\)
\(AB = AC\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow A\) thuộc đường trung trực của \(BC.\)
\( \Rightarrow AO\) là đường trung trực của \(BC\)
\( \Rightarrow AO \bot BC = \left\{ H \right\}\)
\( \Rightarrow H\) là trung điểm của \(BC\) (mối liên hệ giữa đường kính và dây cung).
Áp dụng định lý Pitago cho \(\Delta ABO\) vuông tại \(B\) ta có:
\(AB = \sqrt {A{O^2} - O{B^2}} = \sqrt {9{R^2} - {R^2}} = 2\sqrt 2 R.\)
Áp dụng hệ thức lượng cho \(\Delta ABO\) vuông tại \(B\) có đường cao \(BH\) ta có:
\(\begin{array}{l}BH = \dfrac{{OB.AB}}{{AO}} = \dfrac{{2\sqrt 2 R.R}}{{3R}} = \dfrac{{2\sqrt 2 R}}{3}.\\AH = \dfrac{{A{B^2}}}{{AO}} = \dfrac{{8{R^2}}}{{3R}} = \dfrac{{8R}}{3}\\ \Rightarrow BC = 2BH = \dfrac{{4\sqrt 2 }}{3}R.\\ \Rightarrow {S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.\dfrac{{8R}}{3}.\dfrac{{4\sqrt 2 R}}{3} = \dfrac{{16\sqrt 2 {R^2}}}{9}\,\,\,\,\left( {dvdt} \right).\end{array}\)
Vậy khi \(OA = 3R\) thì \({S_{ABC}} = \dfrac{{16\sqrt 2 {R^2}}}{9}.\)