Đề thi vào 10 môn Toán Thái Nguyên năm 2019
Tải vềCâu 1: Chứng minh
Đề bài
Câu 1: Chứng minh \(A = \sqrt {2\sqrt 5 + 6} - \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} + 2018\) là một số nguyên.
Câu 2: Rút gọn biểu thức \(P = \dfrac{{a - 1}}{{\sqrt b - 1}}\sqrt {\dfrac{{b - 2\sqrt b + 1}}{{{a^2} - 2a + 1}}} \) với \(a < 1\) và \(b > 1\).
Câu 3: Tìm các giá trị của \(m \ne \dfrac{1}{2}\) để hàm số \(y = \left( {2m - 1} \right){x^2}\) đạt giá trị lớn nhất bằng \(0\) tại \(x = 0\).
Câu 5: Một địa phương cấy \(10ha\) giống lúa loại \(I\) và \(8ha\) giống lúa loại \(II\). Sau một mùa vụ, địa phương đó thu hoạch và tính toán sản lượng thấy:
+ Tổng sản lượng của hai giống lúa thu về là \(139\) tấn;
+ Sản lượng thu về từ \(4ha\) giống lúa loại \(I\) nhiều hơn sản lượng thu về từ \(3ha\) giống lúa loại \(II\) là \(6\) tấn.
Hãy tính năng suất lúa trung bình (đơn vị: tấn/ha) của mỗi loại giống lúa.
Câu 6: Cho phương trình \({x^2} - 4x + m + 1 = 0\). Tìm \(m\) để phương trình có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 - 10{x_1}{x_2} = 2020\).
Câu 7: Cho tam giác \(ABC\) vuông tại \(A\) , đường cao \(AH\) . Biết \(AB = 10cm;\,AH = 6cm\). Tính độ dài các cạnh \(AC,BC\) của tam giác \(ABC\).
Câu 8: Cho đường tròn \(\left( O \right)\). Đường thẳng \(d\) tiếp xúc với \(\left( O \right)\) tại \(A\). Trên \(d\) lấy một điểm \(B\,\,\,\left( {B \ne A} \right),\) vẽ đường tròn \(\left( {B,BA} \right)\) cắt đường tròn \(\left( O \right)\) tại điểm \(C\,\,\,\left( {C \ne A} \right).\) Chứng minh \(BC\) là tiếp tuyến của \(\left( O \right)\).
Câu 9: Cho tam giác \(ABC\,\left( {AB < AC} \right)\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right).\) Lấy các điểm \(P,Q\) lần lượt thuộc các cung nhỏ \(AC\) và \(AB\) sao cho \(BP\) vuông góc với \(AC,CQ\) vuông góc với \(AB.\) Gọi \(I,J\) lần lượt là giao điểm của \(PQ\) với \(AB\) và \(AC.\) Chứng minh \(IJ.AC = AI.CB.\)
Câu 10: Từ điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) kẻ các tiếp tuyến \(AB,AC\) đến đường tròn \((B,C\) là tiếp điểm). Gọi \(H\) là giao điểm của \(OA\) và \(BC\).
a) Chứng minh \(O{B^2} = OH.OA\)
b) \(EF\) là một dây cung của \(\left( O \right)\) đi qua \(H\) sao cho \(A,E,F\) không thẳng hàng.
Chứng minh bốn điểm \(A,E,O,F\) nằm trên cùng một đường tròn.
Lời giải chi tiết
Câu 1
Phương pháp:
Rút gọn \(A\), sử dụng hẳng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\).
Cách giải:
Ta có :
\(\begin{array}{l}A = \sqrt {2\sqrt 5 + 6} - \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} + 2018\\A = \sqrt {{1^2} + 2.\sqrt 5 .1 + {{\left( {\sqrt 5 } \right)}^2}} - \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} + 2018\\A = \sqrt {{{\left( {1 + \sqrt 5 } \right)}^2}} - \left| {\sqrt 5 - 1} \right| + 2018\\A = \left| {1 + \sqrt 5 } \right| - \left| {\sqrt 5 - 1} \right| + 2018\\A = 1 + \sqrt 5 - \sqrt 5 + 1 + 2018\,\,\left( {Do\,\,1 + \sqrt 5 > 0;\,\,\sqrt 5 - 1 > 0} \right)\\A = 2020\,\\ \Rightarrow A \in \mathbb{Z}\end{array}\)
Vậy \(A\) là một số nguyên.
Câu 2
Phương pháp:
+) Sử dụng hằng đẳng thức.
+) Xét dấu, phá trị tuyệt đối và rút gọn.
Cách giải:
Với \(a < 1\) và \(b > 1\) ta có:
\(\begin{array}{l}P = \dfrac{{a - 1}}{{\sqrt b - 1}}\sqrt {\dfrac{{b - 2\sqrt b + 1}}{{{a^2} - 2a + 1}}} = \dfrac{{a - 1}}{{\sqrt b - 1}}\sqrt {\dfrac{{{{\left( {\sqrt b - 1} \right)}^2}}}{{{{\left( {a - 1} \right)}^2}}}} = \dfrac{{a - 1}}{{\sqrt b - 1}}.\left| {\dfrac{{\sqrt b - 1}}{{a - 1}}} \right|\\Do\,\,\left\{ \begin{array}{l}a < 1 \Rightarrow a - 1 < 0\\b > 1 \Rightarrow \sqrt b > 1 \Leftrightarrow \sqrt b - 1 > 0\end{array} \right.\\ \Rightarrow \dfrac{{\sqrt b - 1}}{{a - 1}} < 0 \Leftrightarrow \left| {\dfrac{{\sqrt b - 1}}{{a - 1}}} \right| = - \dfrac{{\sqrt b - 1}}{{a - 1}}\\ \Rightarrow A = - \dfrac{{a - 1}}{{\sqrt b - 1}}.\dfrac{{\sqrt b - 1}}{{a - 1}} = - 1\end{array}\)
Câu 3
Phương pháp:
Hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\) đạt giá trị lớn nhất bằng \(0\) tại \(x = 0\) khi \(a < 0.\)
Cách giải:
Ta thấy hàm số \(y = \left( {2m - 1} \right){x^2}\,\,\left( {m \ne \dfrac{1}{2}} \right)\) đạt giá trị lớn nhất bằng \(0\) tại \(x = 0\)
\( \Leftrightarrow 2m - 1 < 0 \Leftrightarrow m < \dfrac{1}{2}\)
Vậy \(m < \dfrac{1}{2}\) thỏa mãn bài toán.
Câu 4
Phương pháp:
Đồ thị hàm số song song với đường thẳng \(y = 2x + 2019\)suy ra \(\left\{ \begin{array}{l}a = 0\\b \ne 2019\end{array} \right..\)
Đồ thị hàm số cắt trục tung tại điểm có tung độ là 2020, suy ra tọa độ giao điểm \(A\left( {0;2020} \right)\) Thay tọa độ giao điểm vào \(y = 2x + b\) ta tìm được b.
Cách giải :
Vì đồ thị hàm số \(y = ax + b\) song song với đường thẳng \(y = 2x + 2019\) nên \(\left\{ \begin{array}{l}a = 0\\b \ne 2019\end{array} \right..\)
\( \Rightarrow y = ax + b \Leftrightarrow y = 2x + b\,\,\,\left( {b \ne 2019} \right)\)
Mà đồ thị hàm số cắt trục tung tại điểm có tung độ là \(2020 \Rightarrow \) đồ thị hàm số đi qua điểm \(\left( {0;\,\,\,2020} \right)\)
\(\begin{array}{l} \Rightarrow 2020 = 2.0 + b\\ \Rightarrow b = 2020\,\,\,\left( {tm} \right)\end{array}\)
Vậy \(a = 2;\,\,\,\,b = 2020.\)
Câu 5
Phương pháp:
- Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
- Bước 2: Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
- Bước 3: Lập hệ phương trình.
- Bước 4: Giải hệ phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Gọi sản lượng lúa của loại I và II trên mỗi \(ha\) lần lượt là \(x\) và \(y\) (tấn/ha). Điều kiện: \(x,y > 0\).
\(10ha\) giống lúa loại I thu về sản lượng \(10x\) tấn; \(8ha\) giống lúa loại II thu về sản lượng \(8y\) tấn
Tổng sản lượng thu về là \(139\) tấn nên ta có phương trình: \(10x + 8y = 139\,\,\left( 1 \right)\).
\(4ha\) giống lúa loại I thu về sản lượng \(4x\) tấn; \(3ha\) giống lúa loại II thu về sản lượng \(3y\) tấn.
Sản lượng thu về từ \(4ha\) giống lúa loại \(I\) nhiều hơn sản lượng thu về từ \(3ha\) giống lúa loại \(II\) là \(6\) tấn nên ta có phương trình: \(4x - 3y = 6\,\,\left( 2 \right)\).
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}10x + 8y = 139\\4x - 3y = 6\end{array} \right.\)
Giải hệ: \(\left\{ \begin{array}{l}10x + 8y = 139\\4x - 3y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}20x + 16y = 278\\20x - 15y = 30\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}31y = 248\\4x - 3y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 8\\x = 7,5\end{array} \right.\left( {TM} \right)\)
Vậy năng suất lúa trung bình của giống lúa loại I là \(7,5\) tấn/ha; năng suất lúa trung bình của giống lúa loại II là \(8\) tấn/ha.
Câu 6
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' \ge 0\end{array} \right.\)
Biến đổi để xuất hiện tổng và tích hai nghiệm rồi sử dụng hệ thức Vi-et.
Cách giải:
Phương trình \({x^2} - 4x + m + 1 = 0\) (*) có \(\Delta ' = {\left( { - 2} \right)^2} - 1.\left( {m + 1} \right) = 3 - m\)
Để phương trình (*) có hai nghiệm \({x_1},{x_2}\) thì \(\left\{ \begin{array}{l}a \ne 0\\\Delta ' \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\\3 - m \ge 0\end{array} \right. \Leftrightarrow m \le 3\)
Theo hệ thức Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}{x_2} = m + 1\end{array} \right.\)
Theo bài ra ta có:
\(\begin{array}{l}x_1^2 + x_2^2 - 10{x_1}{x_2} = 2020\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 12{x_1}{x_2} = 2020\\ \Leftrightarrow {4^2} - 12\left( {m + 1} \right) = 2020\\ \Leftrightarrow 12m = - 2016\\ \Leftrightarrow m = - 168\,\,\left( {tm} \right)\end{array}\)
Vậy \(m = - 168\) là giá trị cần tìm.
Câu 7:
Phương pháp:
+ Áp dụng định lý Py-ta-go trong tam giác vuông. Tính BH
+ Sử dụng hệ thức lượng trong tam giác. Tính BC
+ Áp dụng định lý Py-ta-go cho tam giác ABC. Tính AC.
Cách giải:

Áp dụng định lý Py-ta-go cho tam giác \(ABH\) vuông tại H. Ta có:
\(\begin{array}{l}A{H^2} + B{H^2} = A{B^2}\\ \Rightarrow B{H^2} = A{B^2} - A{H^2} = {10^2} - {6^2} = 100 - 36 = 64\\ \Rightarrow B{H^2} = {8^2}\\ \Rightarrow BH = 8\,\left( {cm} \right)\end{array}\)
Trong tam giác vuông \(ABC\) vuông tại \(A\) có AH là đường cao
\(\begin{array}{l} \Rightarrow A{B^2} = BH.BC\\ \Rightarrow BC = \dfrac{{A{B^2}}}{{BH}} = \dfrac{{{{10}^2}}}{8} = \dfrac{{100}}{8} = 12,5\,\left( {cm} \right)\end{array}\)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(\begin{array}{l}A{C^2} = B{C^2} - A{B^2} = 12,{5^2} - {10^2} = 56,25\\ \Rightarrow AC = 7,5\,\,\,\,\left( {cm} \right).\end{array}\)
Vậy: \(AC = 7,5\,\left( {cm} \right);\,\,\,\,BC = 12,5\,\left( {cm} \right).\)
Câu 8
Phương pháp:
Chứng minh \(\Delta OAB = \Delta OCB\left( {c.c.c} \right)\) và suy ra điều phải chứng minh.
Cách giải:

\(d\) là tiếp tuyến với \(\left( O \right)\) tại \(A\) \( \Rightarrow OA \bot d \Rightarrow \angle OAB = {90^0}\)
\(C = \left( O \right) \cap \left( {B,BA} \right) \Rightarrow \left\{ \begin{array}{l}BC = BA\\OC = OA\end{array} \right.\) (cùng là các bán kính).
Xét tam giác \(OAB\) và \(OCB\) có:
\(\left. \begin{array}{l}BC = BA\\OC = OA\\OB\,\,chung\end{array} \right\} \Rightarrow \Delta OAB = \Delta OCB\left( {c - c - c} \right) \Rightarrow \angle OCB = \angle OAB = {90^0}\)
\( \Rightarrow OC \bot BC\) hay \(BC\) là tiếp tuyến của đường tròn \(\left( O \right)\) (đpcm).
Câu 9
Phương pháp:
+ Góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn
+ Góc nội tiếp có số đo bằng nửa số đo cung bị chắn.
+ Chứng minh hai tam giác \(AIJ\) và tam giác \(ACB\) đồng dạng để suy ra hệ thức cần chứng minh.
Cách giải:
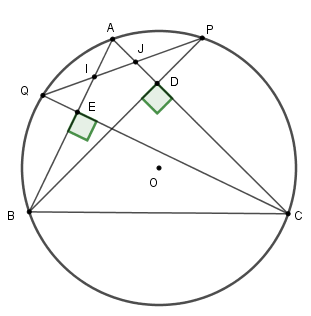
Gọi \(BP \cap AC = \left\{ D \right\};\,\,AB \cap CQ = \left\{ E \right\}.\)
Xét đường tròn \(\left( O \right)\) ta có:
\(\angle BDC = \dfrac{1}{2}\,\,\,\left( {sd\,\,cung\,\,\,BC + \,\,sd\,\,AP} \right)\)
\(\angle BEC = \dfrac{1}{2}\left( {sd\,\,cung\,\,BC + \,\,sd\,\,\,AQ} \right)\,\,\,\left( 1 \right)\) (góc có đỉnh bên trong đường tròn)
Mà theo giả thiết thì \(BD \bot AC\) tại \(D,\) \(CQ \bot AB\) tại \(E \Rightarrow \angle BDC = \angle BEC = {90^0}\,\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra: \(sd\,\,cung\,\,AP = sd\,\,\,cung\,\,\,AQ\,\,\,\,\left( 3 \right).\)
Ta lại có: \(\angle AIJ = \dfrac{1}{2}\left( {sd\,\,cung\,\,\,BQ + sd\,\,\,cung\,\,\,AP} \right)\,\,\,\left( 4 \right)\) (góc có đỉnh bên trong đường tròn)
Và \(\angle ACB = \dfrac{1}{2}sd\,\,cung\,\,\,AB = \dfrac{1}{2}\left( {sd\,\,\,cung\,\,BQ + sd\,\,\,cung\,\,AQ} \right)\,\,\,\,\left( 5 \right)\) (góc nội tiếp chắn cung \(AB\))
Từ (3), (4), (5) suy ra \(\angle ACB = \angle AIJ\)
Xét \(\Delta AIJ\) và \(\Delta ACB\) có:
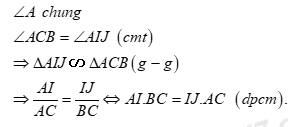
Câu 10:
Phương pháp:
a) Sử dụng hệ thức lượng trong tam giác vuông \(OBA\).
b) Chứng minh hai tam giác \(OHF\) và \(OFA\) đồng dạng suy ra các góc tương ứng bằng nhau.
Từ đó sử dụng dáu hiệu nhận biết của tứ giác nội tiếp để chứng minh tứ giác \(OEAF\) nội tiếp.
Cách giải:
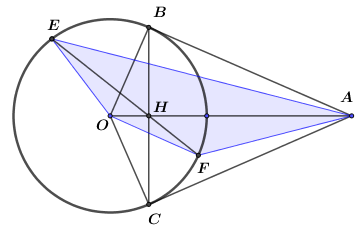
a) Vì \(AB\) là tiếp tuyến của đường tròn \(\left( O \right)\) , \(B\) là tiếp điểm.
\( \Rightarrow AB \bot OB\)
\( \Rightarrow \Delta OBA\) vuông tại B.
Lại có: \(OB = OC \Rightarrow O\) nằm trên trung trực của \(BC\).
\(AB = AC\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow A\) nằm trên trung trực của \(BC\).
Do đó \(AO\) là trung trực của \(BC\) hay \(AO \bot BC\) tại \(H\)\( \Rightarrow BH \bot OA\)
\( \Rightarrow O{B^2} = OH.OA\) (hệ thức lượng trong tam giác vuông \(OBA\))
Vậy: \(O{B^2} = OH.OA\)(đpcm).
b) Theo câu a) \(O{B^2} = OH.OA \Rightarrow \dfrac{{OB}}{{OH}} = \dfrac{{OA}}{{OB}}\)
Mà \(OB = OF\) (cùng bằng bán kính) \( \Rightarrow \dfrac{{OF}}{{OH}} = \dfrac{{OA}}{{OF}}\)
Xét \(\Delta OHF\) và \(\Delta OFA\) có:
\(\angle O\,\,\,\,chung\)
\(\dfrac{{OF}}{{OH}} = \dfrac{{OA}}{{OF}}\left( {cmt} \right)\)
\( \Rightarrow \Delta OHF \sim \Delta OFA\left( {c.g.c} \right) \Rightarrow \angle OAF = \angle OFH = \angle OFE\,\,\left( 1 \right)\) (góc tương ứng)
Mà tam giác \(OEF\) cân tại \(O\) \( \Rightarrow \angle OEF = \angle OFE\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\angle OEF = \angle OAF\left( { = \angle OFE} \right)\)
Xét tứ giác \(AEOF\) có \(\angle OEF = \angle OAF\left( {cmt} \right)\)\( \Rightarrow \) tứ giác \(AEOF\) nội tiếp (tứ giác có hai đinh kề cùng nhìn một cạnh các góc bằng nhau)
Hay bốn điểm \(A,O,E,F\) cùng thuộc một đường tròn (đpcm).