Đề thi vào 10 môn Toán Yên Bái năm 2022 — Không quảng cáo

Đề bài

Câu 1: Cho \(\Delta ABC\) vuông tại A, có AB = 3 và AC = 4. Khi đó độ dài của BC bằng:

A. 1 B. 25 C. 7 D. 5

Câu 2: Nghiệm của phương trình \(2x + 1 = 0\) là:

A. \(x = \dfrac{1}{2}\) B. \(x = 2\) C. \(x = 1\) D. \(x = \dfrac{{ - 1}}{2}\)

Câu 3: Kết quả của phép toán \(\left( {x + 1} \right)\left( {x - 2} \right)\) bằng:

A. \({x^2} - x + 2\) B. \({x^2} - 3x + 2\) C. \({x^2} - x - 2\) D. \({x^2} + x - 2\)

Câu 4: Trong một đường tròn, góc nội tiếp chắn cung \({80^0}\) có số đo bằng:

A. \({20^0}\) B. \({100^0}\) C. \({160^0}\) D. \({40^0}\)

Câu 5: Khẳng định nào sau đây là đúng?

A. \(\sin {37^0} = \cos {53^0}\) B. \(\sin {37^0} = \cos {43^0}\) C. \(\sin {37^0} = \tan {53^0}\) D. \(\sin {37^0} = \cot {53^0}\)

Câu 6: Đường thẳng đi qua điểm A(0; 4) và song song với đường thẳng \(y = \dfrac{1}{3}x - 7\) có phương trình là:

A. \(y = \dfrac{1}{3}x + 4\) B. \(y =  - 3x + 4\) C. \(y =  - 3x - 4\) D. \(y =  - \dfrac{1}{3}x + 4\)

Câu 7: Đồ thị hàm số \(y =  - 2022{x^2}\) đi qua điểm nào trong các điểm sau đây?

A. N(-1; 2022) B. Q(0; -2022) C. P(0;2022) D. M(-1;-2022)

Câu 8: Điều kiện của x để biểu thức \(\sqrt {5 - x} \) có nghĩa là:

A. \(x > 5\) B. \(x \ne 5\) C. \(x \le 5\) D. \(x \ge 5\)

Câu 9: Phương trình nào sau đây không phải là phương trình bậc nhất hai ẩn?

A. \(x + 3y =  - 1\) B. \( - x + 10y = 5\) C. \(\dfrac{1}{x} - 3y =  - 2\) D. \(x + 2y =  - 1\)

Câu 10: Điểm nào sau đây thuộc đồ thị hàm số \(y = 2x + 2\)?

A. M(0; 2) B. P(1; 0) C. N(-1; 2) D. Q(0; -1)

Câu 11: Điều kiện xác định của biểu thức \(P = \sqrt {x - 1}  + \dfrac{1}{{x - 2}}\) là:

A. \(x > 2\) B. \(x \ge 1\) và \(x \ne 2\) C. \(x \ge 2\) D. \(x \ge 1\)

Câu 12: Cho mặt cầu có thể tích \(V = 288\pi c{m^3}\). Đường kính mặt cầu bằng:

A. 4cm B. 12cm C. 8cm D. 6cm

Câu 13: Nghiệm tổng quát của phương trình \( - x + 3y = 1\) là:

A. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = x + 1\end{array} \right.\) B. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y =  - \dfrac{1}{3}x + \dfrac{1}{3}\end{array} \right.\) C. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y =  - \dfrac{1}{3}x + \dfrac{1}{3}\end{array} \right.\) D. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \dfrac{1}{3}x + \dfrac{1}{3}\end{array} \right.\)

Câu 14: Cho hai số x; y thỏa mãn \(\dfrac{x}{2} = \dfrac{y}{5}\) và \(x + y = 14\). Giá trị của x là:

A. x = -4 B. x = 10 C. x = 4 D. x = -10

Câu 15: Số phần tử của tập hợp \(A = \left\{ {a;b;c;d} \right\}\) là:

A. 5 B. 4 C. 3 D. 2

Câu 16: Cho hàm số \(y = \left( {m - 1} \right){x^2}\). Các giá trị của tham số m để đồ thị hàm số đã cho là một parabol nằm phía dưới trục hoành.

A. \(m > 1\) B. \(m \ne 1\) C. \(m = 1\) D. \(m < 1\)

Câu 17: Đường thẳng đi qua hai điểm P(-1; 4) và Q(2; -5) có phương trình là:

A. \(y =  - 3x + 1\) B. \(y =  - 2x - 1\) C. \(y = x - 3\) D. \(y = x + 3\)

Câu 18: Cho \(\cos \alpha  = \dfrac{3}{5}\) với \({0^0} < \alpha  < {90^0}\). Giá trị của \(\tan \alpha \) bằng:

A. \(\dfrac{4}{3}\) B. \(\dfrac{3}{4}\) C. \(\dfrac{4}{5}\) D. \(\dfrac{5}{3}\)

Câu 19: Cho hai điểm A, B thuộc đường tròn (O). Biết \(\angle AOB = {55^0}\). Số đo cung nhỏ AB bằng:

A. \({35^0}\) B. \({55^0}\) C. \({110^0}\) D. \({135^0}\)

Câu 20: Cho hai đường tròn (O; 3cm) và (O’; 2cm). Biết OO’ = 4cm. Vị trí tương đối của (O) và (O’) là:

A. không có điểm chung B. cắt nhau C. tiếp xúc trong D. tiếp xúc ngoài

Câu 21: Công thức tính thể tích V của hình trụ có bán kính đáy r, chiều cao h là:

A. \(V = \dfrac{1}{3}\pi {r^2}h\) B. \(V = \pi {r^2}h\) C. \(V = \dfrac{1}{2}\pi rh\) D. \(V = 2\pi rh\)

Câu 22: Cho \(\Delta ABC\) vuông tại A có \(\angle ABC = {30^0}\) và BC = 4cm. Độ dài cạnh AC bằng:

A. 2cm B. 6cm C. \(2\sqrt 3 cm\) D. \(4\sqrt 3 cm\)

Câu 23: Cho đường tròn (O; 25cm). Dây lớn nhất của đường tròn có độ dài bằng:

A. 25cm B. 20cm C. 50cm D. \(625\sqrt 3 cm\)

Câu 24: Số ước nguyên dương của 24 là:

A. 12 B. 4 C. 8 D. 24

Câu 25: Giá trị lớn nhất của biểu thức \(M =  - {x^2} + 4x - 10\) bằng:

A. -5 B. 4 C. -6 D. 0

Câu 26: Cho nửa đường tròn đường kính AB và điểm C thuộc đường tròn sao cho sđ cung AC \( = {110^0}\). Kẻ tiếp tuyến Ax với nửa đường tròn (hình vẽ). Số đo góc hợp bởi hai tia Ax và AC là:

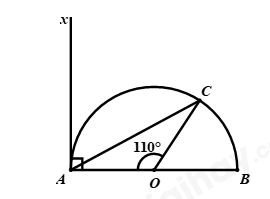
A. \({70^0}\) B. \({35^0}\) C. \({110^0}\) D. \({55^0}\)

Câu 27: Cho đường tròn (O; 5cm). Khoảng cách từ tâm O đến đường thẳng d là 6cm. Số điểm chung của đường thẳng d và đường tròn là:

A. vô số B. 1 C. 0 D. 2

Câu 28: Biểu thức \({2^3}{.2^4}{.2^5}\) có giá trị bằng:

A. \({2^7}\) B. \({2^{12}}\) C. \({2^9}\) D. \({2^{60}}\)

Câu 29: Hệ số góc của đường thẳng \(y = 5x - 1\) là:

A. -1 B. 1 C. 5 D. -5

Câu 30: Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \(2{x^2} - 3x + 1 = 0\). Khi đó

A. \({x_1}{x_2} =  - \dfrac{3}{2}\) B. \({x_1}{x_2} =  - \dfrac{1}{2}\) C. \({x_1}{x_2} = \dfrac{3}{2}\) D. \({x_1}{x_2} = \dfrac{1}{2}\)

Câu 31: Giá trị của biểu thức \(\sqrt {25}  - 3\) bằng:

A. 16 B. 22 C. 2 D. -8

Câu 32: Hàm số nào dưới đây đồng biến trên \(\mathbb{R}?\)

A. \(y =  - 2x + 3\) B. \(y =  - 3 - x\) C. \(y = 3 - 4x\) D. \(y = 2x + 1\)

Câu 33: Số nghiệm của phương trình \({x^2} - 6x + 10 = 0\) là:

A. 0 B. 3 C. 2 D. 1

Câu 34: Cho tứ giác nội tiếp ABCD có \(\angle A = {70^0}\) và \(\angle B = {60^0}\). Khẳng định nào sau đây đúng?

A. \(\angle D = {110^0}\) B. \(\angle C = {120^0}\) C. \(\angle D = {130^0}\) D. \(\angle C = {110^0}\)

Câu 35: Giá trị của biểu thức \(\dfrac{{\sqrt 8  - \sqrt {27} }}{{\sqrt 2  - \sqrt 3 }} - \sqrt 6 \) bằng:

A. \(5 + 2\sqrt 6 \) B. \(1\) C. \(5\) D. \(5 - 2\sqrt 6 \)

Câu 36: Kết quả của biểu thức \(A = \dfrac{{4x}}{{x - 9}} + \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 3}} - \dfrac{{\sqrt x  - 3}}{{\sqrt x  + 3}}\) (với \(x \ge 0;x \ne 9\)) có dạng \(\dfrac{{m\sqrt x  + n}}{{\sqrt x  - 3}}\) với \(m,n \in \mathbb{R}\). Giá trị của biểu thức \(m - n\) là:

A. 4 B. -4 C. 2 D. 3

Câu 37: Cho hai đường tròn (O; 12cm) và (I; 16cm) cắt nhau tại hai điểm A, B. Biết AB = 19,2cm. Khoảng cách OI bằng:

A. 20cm B. 9,8cm C. 9,6cm D. 5,6cm

Câu 38: Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 2mx - m + 3\). Giá trị của tham số m để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ \({x_1};{x_2}\) thỏa mãn \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{3}{2}\) là:

A. m = 6 B. m = 9 C. m = -6 D. m = -9

Câu 39: Giá trị của tham số m để hệ phương trình \(\left\{ \begin{array}{l}2x + y = 5m + 1\\x + 3y = 5m + 3\end{array} \right.\) có nghiệm duy nhất (x; y) thỏa mãn \(x - y = 5\) là:

A. m = 6 B. m = 4 C. m = 3 D. m = -2

Câu 40: Cho \(\Delta ABC\) vuông tại A, đường cao \(AH\left( {H \in BC} \right)\). Biết HB = 12,5cm và \(\angle B = {65^0}\). Độ dài cạnh AC (kết quả làm tròn đến chữ số thứ hai phân thập phân) bằng:

A. 64,41cm B. 63,43cm C. 13,78cm D. 25cm

Câu 41: Số nghiệm của phương trình \(2{x^4} - 3{x^2} - 20 = 0\) là:

A. 1 B. 2 C. 4 D. 0

Câu 42: Khoảng cách từ gốc tọa độ O(0; 0) đến đường thẳng 4x – 3y + 10 = 0 bằng:

A. 10 B. 5 C. 2 D. 4

Câu 43: Cho phương trình \({x^2} - 2x - m + 1 = 0\). Điều kiện của m để phương trình đã cho có hai nghiệm trái dấu là:

A. m > 3 B. m < -1 C. m > 1 D. m > 2

Câu 44: Cho đường thẳng y = ax + b song song với đường thẳng y = 4x – 3 đồng thời cắt trục Ox tại A, cắt trục Oy tại B. Biết diện tích \(\Delta OAB\) bằng 2. Giá trị của biểu thức \(T = {a^2} + {b^2}\) là:

A. T = 40 B. T = 24 C. T = 32 D. T = 16

Câu 45: Cho đường tròn (O; 15cm), dây AB = 24cm. Một tiếp tuyến song song với AB cắt các tia OA; OB theo thứ tự E và F. Độ dài EF bằng:

A. 48cm B. 42cm C. 40cm D. 20cm

Câu 46: Cho đường tròn (O) đường kính \(AB = 2\sqrt 3 \,cm\) và C là điểm chính giữa của cung AB. Cung AmB có tâm C, bán kính CA (hình vẽ). Diện tích phần gạch chéo bằng:

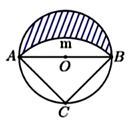
A. \(\dfrac{9}{4}\,c{m^2}\) B. \(\dfrac{{4\pi }}{3}\,c{m^2}\) C. \(3\pi c{m^2}\) D. \(3c{m^2}\)

Câu 47: Số các giá trị của tham số m để phương trình \({x^2} - 2mx + 2m + 3 = 0\) có hai nghiệm nguyên phân biệt là:

A. 3 B. 1 C. 2 D. 4

Câu 48: Từ hai vị trí A, B của một tòa nhà, người ta dùng một dụng cụ quan sát đỉnh C của ngọn núi (hình vẽ). Biết rằng chiều cao AB của tòa nhà là 70m, phương nhìn AC tạo với phương ngang góc \({30^0}\), phương nhìn BC tạo với phương ngang góc \({15^0}30'\). Ngọn núi đó có chiều cao so với mặt đất gần với kết quả nào sau đây nhất?

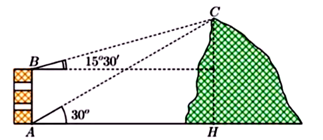
A. 145m B. 140m C. 135m D. 130m

Câu 49: Cho hình bình hành ABCD (\(\angle A > {90^0}\)). Gọi M, N, P lần lượt là hình chiếu của C lên AD, DB và AB. Biết MN = 5 và NP = 4. Độ dài đoạn CN gần với kết quả nào sau đây nhất?

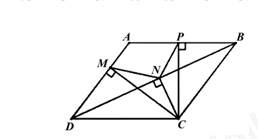
A. 4,4 B. 4,6 C. 4,8 D. 4,2

Câu 50: Cho các số dương x, y, z thỏa mãn \(x\sqrt {1 - {y^2}}  + y\sqrt {1 - {z^2}}  + z\sqrt {1 - {x^2}}  = \dfrac{3}{2}\). Giá trị của biểu thức \(P = {x^4} + {y^4} + {z^4}\) là:

A. \(1\) B. \(\dfrac{1}{4}\) C. \(\dfrac{3}{4}\) D. \(\dfrac{1}{2}\)

Lời giải

BẢNG ĐÁP ÁN

Câu 1 (NB):

Phương pháp:

Áp dụng định lý Py – ta – go.

Cách giải:

Tam giác ABC vuông tại A, theo định lý Py – ta – go, ta có:

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ \Leftrightarrow B{C^2} = {3^2} + {4^2} = 25\\ \Leftrightarrow B{C^2} = {5^2}\\ \Rightarrow BC = 5\end{array}\)

Vậy BC = 5

Chọn D.

Câu 2 (NB):

Phương pháp:

Giải phương trình: \(ax + b = 0\left( {a \ne 0} \right) \Leftrightarrow x = \dfrac{{ - b}}{a}\)

Cách giải:

\(\begin{array}{l}2x + 1 = 0\\ \Leftrightarrow 2x =  - 1\\ \Leftrightarrow x = \dfrac{{ - 1}}{2}\end{array}\)

Vậy \(x =  - \dfrac{1}{2}\)

Chọn D.

Câu 3 (NB):

Phương pháp:

Thực hiện \(\left( {A + B} \right)\left( {C + D} \right) = AC + AD + BC + BD\)

Cách giải:

\(\left( {x + 1} \right)\left( {x - 2} \right)\)\( = {x^2} - 2x + x - 2 = {x^2} - x - 2\)

Chọn C.

Câu 4 (NB):

Phương pháp:

Số đo góc nội tiếp \( = \dfrac{1}{2}\) số đo cung chắn

Cách giải:

Góc nội tiếp có số đo là: \(\dfrac{1}{2}{.80^0} = {40^0}\)

Chọn D.

Câu 5 (NB):

Phương pháp:

\(\sin \left( {{{90}^0} - \alpha } \right) = \cos \alpha \)

Cách giải:

\(\sin {37^0} = \sin \left( {{{90}^0} - {{53}^0}} \right) = \cos {53^0}\)

Chọn A.

Câu 6 (TH):

Phương pháp:

Viết phương trình đường thẳng \(\Delta \) biết \(\Delta \) đi qua điểm \(A\left( {{x_A};{y_A}} \right)\) và song song với \(d:y = a'x + b'\) (\(a';b'\)  đã biết)

Bước 1: Gọi phương trình đường thẳng\(\Delta \) là \(y = ax + b\)

Bước 2: Vì \(\Delta //d \Rightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\)\( \Rightarrow d:y = a'x + b\)

Bước 3: \(\Delta \) đi qua điểm \(A\left( {{x_A};{y_A}} \right)\), từ đó tìm được \(b\), đối chiếu điều kiện ở trên

Bước 4: Kết luận phương trình đường thẳng cần tìm.

Cách giải:

Gọi phương trình đường thẳng cần tìm là: \(y = ax + b\)

Vì đường thẳng cần tìm song song với đường thẳng \(y = \dfrac{1}{3}x - 7\) nên \(\left\{ \begin{array}{l}a = \dfrac{1}{3}\\b \ne  - 7\end{array} \right.\)

Do đó, phương trình cần tìm có dạng: \(y = \dfrac{1}{3}x + b\,\,\left( {b \ne  - 7} \right)\)

Vì đường thẳng cần tìm đi qua điểm A(0; 4) nên ta có: \(4 = \dfrac{1}{3}.0 + b \Rightarrow b = 4\) (tmđk)

Vậy phương trình đường thẳng cần tìm là: \(y = \dfrac{1}{3}x + 4\)

Chọn A.

Câu 7 (NB):

Phương pháp:

Đồ thị hàm số \(\left( P \right):y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) khi \(\left( P \right):{y_A} = a{x_A}^2\left( {a \ne 0} \right)\)

Cách giải:

+ Thay \(x =  - 1\) vào \(y =  - 2022{x^2}\), ta được: \(y =  - 2022.{\left( { - 1} \right)^2} =  - 2022\)

Suy ra đồ thị hàm số \(y =  - 2022{x^2}\) đi quả điểm M(-1; -2022)

Chọn D.

Câu 8 (NB):

Phương pháp:

Biểu thức \(\sqrt {f\left( x \right)} \) có nghĩa \( \Leftrightarrow f\left( x \right) \ge 0\)

Cách giải:

Biểu thức \(\sqrt {5 - x} \) có nghĩa \(5 - x \ge 0 \Leftrightarrow x \le 5\)

Vậy biểu thức \(\sqrt {5 - x} \) có nghĩa khi \(x \le 5\)

Chọn C.

Câu 9 (NB):

Phương pháp:

Phương trình bậc nhất hai ẩn có dạng: \(ax + by = c\)

Cách giải:

Phương trình: \(\dfrac{1}{x} - 3y =  - 2\) không là phương trình bậc nhất hai ẩn.

Chọn C.

Câu 10 (NB):

Phương pháp:

Đường thẳng \(\left( d \right):y = ax + b\) đi qua điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) khi \({y_A} = a{x_A} + b\).

Cách giải:

Thay x = 0 vào \(y = 2x + 2\), ta được: y = 2.0 + 2 = 2

Vậy điểm M(0; 2) thuộc đồ thị hàm số \(y = 2x + 2\).

Chọn A.

Câu 11 (TH):

Phương pháp:

Biểu thức \(\sqrt {f\left( x \right)} \) có nghĩa \( \Leftrightarrow f\left( x \right) \ge 0\)

Biểu thức \(\dfrac{1}{{g\left( x \right)}}\) có nghĩa \( \Leftrightarrow g\left( x \right) \ne 0\)

Cách giải:

Điều kiện xác định của biểu thức P là: \(\left\{ \begin{array}{l}x - 1 \ge 0\\x - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \ne 2\end{array} \right.\)

Vậy điều kiện xác định của biểu thức P là: \(x \ge 1\) và \(x \ne 2\)

Chọn B.

Câu 12 (TH):

Phương pháp:

Thể tích của mặt cầu có bán kính R là: \(V = \dfrac{4}{3}\pi {R^3}\)

Cách giải:

Gọi R (điều kiện: R > 0) là bán kính của mặt cầu.

Thể tích của mặt cầu là: \(\dfrac{4}{3}\pi {R^3} = 288\pi  \Rightarrow R = 6\) (cm)

Đường kính mặt cầu là: 2R = 2.6 = 12 (cm)

Chọn B.

Câu 13 (NB):

Phương pháp:

Phương trình \(ax + by = c\) (với \(a \ne 0,b \ne 0\)) có nghiệm tổng quát là \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y =  - \dfrac{a}{b}x + \dfrac{c}{b}\end{array} \right.\)

Cách giải:

Phương trình \( - x + 3y = 1\) có nghiệm tổng quát là: \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \dfrac{1}{3}x + \dfrac{1}{3}\end{array} \right.\)

Chọn D.

Câu 14 (TH):

Phương pháp:

Áp dụng tính chất của dãy tỉ số bằng nhau.

Cách giải:

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{2} = \dfrac{y}{5} = \dfrac{{x + y}}{{2 + 5}} = \dfrac{{14}}{7} = 2\)

Khi đó, \(\dfrac{x}{2} = 2 \Rightarrow x = 4\)

Vậy x = 4

Chọn C.

Câu 15 (NB):

Phương pháp:

Thực hiện đếm số phần tử của tập hợp A.

Cách giải:

Số phần tử của tập hợp \(A = \left\{ {a;b;c;d} \right\}\) là: 4

Chọn B.

Câu 16 (TH):

Phương pháp:

Đồ thị hàm số \(y = a{x^2}\) nằm phía dưới trục hoành \( \Leftrightarrow y < 0 \Leftrightarrow a < 0\)

Cách giải:

Đồ thị hàm số \(y = \left( {m - 1} \right){x^2}\) nằm phía dưới trục hoành \( \Leftrightarrow m - 1 < 0 \Leftrightarrow m < 1\)

Vậy \(m < 1\)

Chọn D.

Câu 17 (TH):

Phương pháp:

Viết phương trình đường thẳng đi qua hai điểm \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\)

Bước 1: Gọi phương trình đường thẳng cần tìm là: \(y = ax + b\)

Bước 2: Đường thẳng đi qua hai điểm \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\) nên ta có hệ phương trình: \(\left\{ \begin{array}{l}a{x_A} + b = {y_A}\\a{x_B} + b = {y_B}\end{array} \right.\)

Giải hệ phương trình, tìm \(a,b\).

Bước 3: Kết luận phương trình đường thẳng cần tìm.

Cách giải:

Gọi phương trình đường thẳng cần tìm là: \(y = ax + b\)

Đường thẳng đi qua hai điểm P(-1; 4) và Q(2;-5) nên ta có hệ phương trình: \(\left\{ \begin{array}{l}a.\left( { - 1} \right) + b = 4\\a.2 + b =  - 5\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l} - a + b = 4\\2a + b =  - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3a = 9\\ - a + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 3\\b = a + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 3\\b = 1\end{array} \right.\)

Vậy phương trình đường thẳng cần tìm là: \(y =  - 3x + 1\)

Chọn A.

Câu 18 (TH):

Phương pháp:

Tính \(\sin \alpha \), \(\tan \alpha  = \dfrac{{\sin \alpha }}{{\cos \alpha }}\)

Cách giải:

Vì \({0^0} < \alpha  < {90^0} \Rightarrow \sin \alpha  > 0\)

Ta có: \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)

\(\begin{array}{l} \Leftrightarrow {\sin ^2}\alpha  + {\left( {\dfrac{3}{5}} \right)^2} = 1\\ \Leftrightarrow {\sin ^2}\alpha  = 1 - {\left( {\dfrac{3}{5}} \right)^2} = \dfrac{{16}}{{25}}\\ \Rightarrow \sin \alpha  = \dfrac{4}{5}\end{array}\)

Ta có: \(\tan \alpha  = \dfrac{{\sin \alpha }}{{\cos \alpha }} = \dfrac{3}{5}:\dfrac{4}{5} = \dfrac{3}{4}\)

Chọn B.

Câu 19 (NB):

Phương pháp:

Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

Cách giải:

Ta có: \(\angle AOB = {55^0}\) nên số đo cung nhỏ AB bằng \({55^0}\).

Chọn B.

Câu 20 (NB):

Phương pháp:

Vận dụng kiến thức vị trí tương đối của hai đường tròn.

Cách giải:

Ta có: \(3 - 2 < OO' < 3 + 2\) nên hai đường tròn cắt nhau.

Chọn B.

Câu 21 (NB):

Phương pháp:

Công thức tính thể tích V của hình trụ có bán kính đáy r, chiều cao h là: \(V = \pi {r^2}h\)

Cách giải:

Công thức tính thể tích V của hình trụ có bán kính đáy r, chiều cao h là: \(V = \pi {r^2}h\)

Chọn B.

Câu 22 (NB):

Phương pháp:

Vận dụng định lí tỉ số lượng giác của góc nhọn tròng tam giác vuông.

Cách giải:

Tam giác ABC vuông tại A, ta có: \(\sin \angle ABC = \dfrac{{AC}}{{BC}}\) (tỉ số lượng giác của góc nhọn trong tam giác vuông)

\( \Rightarrow AC = BC.\sin \angle ABC = 4.\sin {30^0} = 2\,\left( {cm} \right)\)

Chọn A.

Câu 23 (NB):

Phương pháp:

Dây lớn nhất của đường tròn là đường kính.

Cách giải:

Dây lớn nhất của đường tròn có độ dài bằng: 25cm

Chọn A.

Câu 24 (NB):

Phương pháp:

Giả sử số tự nhiên n được phân tích thành thừa số nguyên tố: \(n = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\)

Khi đó, số ước nguyên dương của n là: \(\left( {{m_1} + 1} \right)\left( {{m_2} + 1} \right)...\left( {{m_k} + 1} \right)\)

Cách giải:

Ta có: \(24 = {2^3}.3\)

Khi đó, số ước nguyên dương của 24 là: \(\left( {3 + 1} \right).\left( {1 + 1} \right) = 8\)

Chọn C.

Câu 25 (TH):

Phương pháp:

Sử dụng hẳng đẳng thức, đánh giá để tìm GTLN của biểu thức.

Cách giải:

\(M =  - {x^2} + 4x - 10\)

\(\begin{array}{l} =  - \left( {{x^2} - 4x + 4} \right) + 4 - 10\\ =  - {\left( {x - 2} \right)^2} - 6\end{array}\)

Vì \( - {\left( {x - 2} \right)^2} \le 0\) với mọi x suy ra \( - {\left( {x - 2} \right)^2} - 6 \le  - 6\) với mọi x hay \(M \le  - 6\) với mọi x

Dấu “=” xảy ra \( \Leftrightarrow x - 2 = 0 \Leftrightarrow x = 2\)

Vậy GTNN của M bằng -6 khi x = 2.

Chọn C.

Câu 26 (TH):

Phương pháp:

Số đo góc tạo bởi tiếp tuyến và dây cung \( = \dfrac{1}{2}\) số đo góc nội tiếp cùng chắn cung đó.

Cách giải:

Góc hợp bởi hai tia Ax và AC là góc xAC

Xét (O) có: \(\angle xAC = \dfrac{1}{2}\angle AOC\) (Số đo góc tạo bởi tiếp tuyến và dây cung \( = \dfrac{1}{2}\) số đo góc nội tiếp cùng chắn cung AC)

Suy ra \(\angle xAC = \dfrac{1}{2}{.110^0} = {55^0}\)

Chọn D.

Câu 27 (NB):

Phương pháp:

Vận dụng kiến thức vị trí của đường thẳng và đường tròn.

Cách giải:

Vì 5cm < 6cm nên R < khoảng cách từ tâm O đến đường thẳng d do đó, số điểm chung của đường thẳng d và đường tròn là 0.

Chọn C.

Câu 28 (NB):

Phương pháp:

Vận dụng công thức: \({a^{{x_1}}}.{a^{{x_2}}}...{a^{{x_n}}} = {a^{{x_1} + {x_2} + ... + {x_n}}}\)

Cách giải:

\({2^3}{.2^4}{.2^5} = {2^{3 + 4 + 5}} = {2^{12}}\)

Chọn B.

Câu 29 (NB):

Phương pháp:

Hệ số góc của đường thẳng \(y = ax + b\) là a.

Cách giải:

Hệ số góc của đường thẳng \(y = 5x - 1\) là: 5

Chọn C.

Câu 30 (NB):

Phương pháp:

Nếu phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\)có hai nghiệm phân biệt \({x_1},{x_2}\) khi đó, áp dụng hệ thức Vi – ét, ta có: \({x_1}.{x_2} = \dfrac{c}{a}\)

Cách giải:

\({x_1},{x_2}\) là hai nghiệm của phương trình \(2{x^2} - 3x + 1 = 0\), áp dụng hệ thức Vi – ét, ta có: \({x_1}{x_2} = \dfrac{1}{2}\)

Chọn D.

Câu 31 (NB):

Phương pháp:

Sử dụng hằng đẳng thức: \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)

Cách giải:

\(\begin{array}{l}\sqrt {25}  - 3 = \sqrt {{5^2}}  - 3\\ = \left| 5 \right| - 3 = 5 - 3\,\,\,\left( {do\,\,5 > 0} \right)\\ = 2\end{array}\)

Chọn C.

Câu 32 (NB):

Phương pháp:

Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0\)

Cách giải:

Hàm số \(y = 2x + 1\) có \(a = 2 > 0\) nên hàm số đồng biến trên \(\mathbb{R}\)

Chọn D.

Câu 33 (NB):

Phương pháp:

Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\), ta có:

+ Nếu \(\Delta  = 0 \Rightarrow \)Phương trình có 1 nghiệm.

+ Nếu \(\Delta  < 0 \Rightarrow \)Phương trình không có nghiệm.

+ Nếu \(\Delta  > 0 \Rightarrow \)Phương trình có 2 nghiệm phân biệt.

Cách giải:

Ta có: \(\Delta ' = {\left( { - 3} \right)^2} - 1.10 =  - 1 < 0 \Rightarrow \)Phương trình vô nghiệm

Vậy số nghiệm của phương trình là 0.

Chọn A.

Câu 34 (NB):

Phương pháp:

Tứ giác nội tiếp có tổng hai góc bằng 180 độ.

Cách giải:

Tứ giác ABCD nội tiếp nên \(\angle A + \angle C = {180^0}\)

\( \Rightarrow \angle C = {180^0} - \angle A = {180^0} - {70^0} = {110^0}\)

Chọn A.

Câu 35 (TH):

Phương pháp:

Rút gọn biểu thức chứa căn bậc hai.

Cách giải:

\(\begin{array}{l}\dfrac{{\sqrt 8  - \sqrt {27} }}{{\sqrt 2  - \sqrt 3 }} - \sqrt 6 \\ = \dfrac{{\sqrt {{2^3}}  - \sqrt {{3^3}} }}{{\sqrt 2  - \sqrt 3 }} - \sqrt 6 \\ = \dfrac{{\left( {\sqrt 2  - \sqrt 3 } \right)\left( {\sqrt {{2^2}}  + \sqrt {2.3}  + \sqrt {{3^2}} } \right)}}{{\sqrt 2  - \sqrt 3 }} - \sqrt 6 \\ = 2 + \sqrt 6  + 3 - \sqrt 6 \\ = 5\end{array}\)

Chọn C.

Câu 36 (VD):

Phương pháp:

Xác định mẫu thức chung, quy đồng thực hiện các phép toán với phân thức đại số.

Cách giải:

\(A = \dfrac{{4x}}{{x - 9}} + \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 3}} - \dfrac{{\sqrt x  - 3}}{{\sqrt x  + 3}}\)

\(\begin{array}{l} = \dfrac{{4x}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}} + \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 3}} - \dfrac{{\sqrt x  - 3}}{{\sqrt x  + 3}}\\ = \dfrac{{4x + {{\left( {\sqrt x  + 3} \right)}^2} - {{\left( {\sqrt x  - 3} \right)}^2}}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\ = \dfrac{{4x + x + 6\sqrt x  + 9 - x + 6\sqrt x  - 9}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\ = \dfrac{{4x + 12\sqrt x }}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\ = \dfrac{{4\sqrt x \left( {\sqrt x  + 3} \right)}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\ = \dfrac{{4\sqrt x }}{{\sqrt x  - 3}}\end{array}\)

Khi đó, m = 4, n = 0 suy ra m – n = 4

Chọn A.

Câu 37 (VD):

Phương pháp:

Áp dụng định lí Py – ta – go để tính độ dài OI

Cách giải:

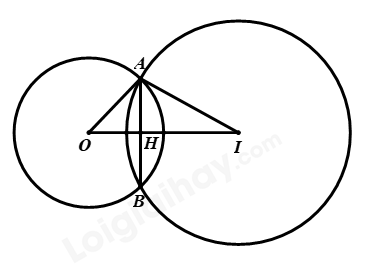
Gọi H là giao điểm của OI và AB

Ta có: AI = BI; OI = OB nên OI là đường trung trực của AB

Suy ra H là trung điểm của \(AB \Rightarrow AH = \dfrac{1}{2}AB = \dfrac{1}{2}.19,2 = 9,6\,\left( {cm} \right)\)

và OI vuông góc với AB tại H

Xét \(\Delta AHI\) vuông tại H, áp dụng định lí Py – ta – go, ta có:

\(\begin{array}{l}A{I^2} = A{H^2} + I{H^2}\\ \Leftrightarrow I{H^2} = A{I^2} - A{H^2}\\ \Leftrightarrow I{H^2} = {16^2} - 9,{6^2} = 163,84\\ \Rightarrow IH = 12,8\left( {cm} \right)\end{array}\)

Xét \(\Delta AOH\) vuông tại H, áp dụng định lí Py – ta – go, ta có:

\(\begin{array}{l}A{O^2} = A{H^2} + O{H^2}\\ \Leftrightarrow O{H^2} = A{O^2} - A{H^2}\\ \Leftrightarrow O{H^2} = {12^2} - 9,{6^2} = 51,84\\ \Rightarrow OH = 7,2\left( {cm} \right)\end{array}\)

Ta có: \(OI = OH + HI = 7,2 + 12,8 = 20\left( {cm} \right)\)

Chọn A.

Câu 38 (VD):

Phương pháp:

Xét phương trình hoành độ giao điểm của (P) và (d)   (1)

Yêu cầu đề bài \( \Leftrightarrow \) phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\)

Theo hệ thức Vi – ét, tính được \({x_1} + {x_2},{x_1}{x_2}\) theo m, sau đó thay vào \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{3}{2}\) để tìm m.

Cách giải:

Xét phương trình hoành độ giao điểm của (P) và (d) ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,\,{x^2} = 2mx - m + 3\\ \Leftrightarrow {x^2} - 2mx + m - 3 = 0\,\,\,\,\,\,\left( 1 \right)\end{array}\)

Để (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ \({x_1};{x_2}\) thì phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\) \( \Leftrightarrow \Delta ' > 0\)

\(\begin{array}{l} \Leftrightarrow {\left( { - m} \right)^2} - 1.\left( {m - 3} \right) > 0\\ \Leftrightarrow {m^2} - m + 3 > 0\\ \Leftrightarrow {m^2} - 2.\dfrac{1}{2}m + {\left( {\dfrac{1}{2}} \right)^2} - {\left( {\dfrac{1}{2}} \right)^2} + 3 > 0\end{array}\)

\( \Leftrightarrow {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{{11}}{4} > 0\) với mọi m

Theo hệ thức Vi – ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = m - 3\end{array} \right.\)

Theo đề bài: \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{3}{2}\) (điều kiện: \({x_1} \ne 0;{x_2} \ne 0 \Rightarrow {x_1}{x_2} \ne 0 \Leftrightarrow m \ne 3\))

\(\begin{array}{l} \Leftrightarrow \dfrac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \dfrac{3}{2}\\ \Rightarrow 2\left( {{x_1} + {x_2}} \right) = 3{x_1}{x_2}\\ \Leftrightarrow 2.2m - 3\left( {m - 3} \right) = 0\\ \Leftrightarrow 4m - 3m + 9 = 0\\ \Leftrightarrow m + 9 = 0\\ \Leftrightarrow m =  - 9\,\,\,\left( {tmdk} \right)\end{array}\)

Chọn D.

Câu 39 (TH):

Phương pháp:

Sử dụng phương pháp cộng đại số tìm nghiệm x, y của hệ phương trình.

Thay nghiệm x, y của hệ phương trình vào \(x - y = 5\) để tìm m

Cách giải:

\(\left\{ \begin{array}{l}2x + y = 5m + 1\\x + 3y = 5m + 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}2x + y = 5m + 1\\2x + 6y = 10m + 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5y = 5m + 5\\x + 3y = 5m + 3\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}y = m + 1\\x = 5m + 3 - 3y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = m + 1\\x = 5m + 3 - 3\left( {m + 1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = m + 1\\x = 2m\end{array} \right.\)

Vậy phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2m;m + 1} \right)\)

Để \(x - y = 5\) \( \Leftrightarrow 2m - \left( {m + 1} \right) = 5\)

\(\begin{array}{l} \Leftrightarrow 2m - m - 1 = 5\\ \Leftrightarrow m - 1 = 5\\ \Leftrightarrow m = 6\end{array}\)

Vậy \(m = 6\)

Chọn A.

Câu 40 (VD):

Phương pháp:

Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.

Cách giải:

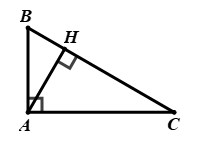
\(\Delta ABH\) vuông tại H, áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có:

\(\tan \angle B = \dfrac{{AH}}{{BH}} \Rightarrow AH = BH.\tan \angle B = 12,5.\tan {65^0}\)

Ta có: \(\angle B = \angle HAC = {65^0}\) (cùng phụ với \(\angle BAH\))

\(\Delta AHC\) vuông tại H, áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có:

\(\cos \angle HAC = \dfrac{{AH}}{{AC}} \Rightarrow AC = \dfrac{{AH}}{{\cos \angle HAC}} = \dfrac{{12,5.\tan {{65}^0}}}{{\cos {{65}^0}}} \approx 63,43\,\left( {cm} \right)\)

Chọn B.

Câu 41 (VD):

Phương pháp:

Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\)

Phương trình ban đầu trở thành phương trình bậc hai một ẩn: \(a{t^2} + bt + c = 0\left( {a \ne 0} \right)\)

Cách giải:

Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\), phương trình ban đầu trở thành: \(2{t^2} - 3t - 20 = 0\)   (1)

Ta có: \({t_1}{t_2} = 2.\left( { - 20} \right) < 0\) suy ra phương trình (1) có hai nghiệm trái dấu t

\( \Rightarrow \) Phương trình ban đầu có hai nghiệm x

Chọn B.

Câu 42 (VD):

Phương pháp:

Áp dụng hệ thức lượng trong tam giác vuông.

Cách giải:

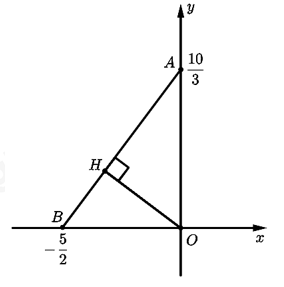
Gọi A là giao điểm của đường thẳng và Oy suy ra \(A\left( {0;\dfrac{{10}}{3}} \right)\)

B là giao điểm của đường thẳng và Ox suy ra \(B\left( {\dfrac{{ - 5}}{2};0} \right)\)

Khi đó, \(OA = \left| {\dfrac{{10}}{3}} \right| = \dfrac{{10}}{3} & \,;\,OB = \left| {\dfrac{{ - 5}}{2}} \right| = \dfrac{5}{2}\)

Kẻ OH vuông góc với AB khi đó khoảng cách từ O (0; 0) đến đường thẳng là OH

\(\Delta OAB\) vuông tại O, đường cao OH, ta có:

\(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}}\)

\(\begin{array}{l} \Leftrightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{{{\left( {\dfrac{{10}}{3}} \right)}^2}}} + \dfrac{1}{{{{\left( { - \dfrac{5}{2}} \right)}^2}}} = \dfrac{1}{4}\\ \Rightarrow O{H^2} = 4\\ \Rightarrow OH = 2\end{array}\)

Chọn C.

Câu 43 (TH):

Phương pháp:

Phương trình \(a{x^2} + bx + c = 0\,\left( {a \ne 0} \right)\) có hai nghiệm trái dấu \( \Leftrightarrow ac < 0\)

Cách giải:

Phương trình đã cho có hai nghiệm trái dấu \( \Leftrightarrow 1.\left( { - m + 1} \right) < 0\)

\(\begin{array}{l} \Leftrightarrow  - m <  - 1\\ \Leftrightarrow m > 1\end{array}\)

Vậy m > 1

Chọn C.

Câu 44 (VD):

Phương pháp:

Đường thẳng \(\left( d \right):y = ax + b\) song song với đường thẳng \(\left( {d'} \right):y = a'x + b'\) khi và chỉ khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\).

Cách giải:

Gọi đường thẳng cần tìm là \(\left( d \right):y = ax + b\)

Đường thẳng y = ax + b song song với đường thẳng y = 4x – 3 nên \(\left\{ \begin{array}{l}a = 4\\b \ne  - 3\end{array} \right.\)

Khi đó, đường thẳng có dạng \(\left( d \right):\,y = 4x + b\,\,\left( {b \ne  - 3} \right)\)

(d) cắt trục Ox tại A nên \(A\left( {\dfrac{{ - b}}{a};0} \right)\) suy ra \(OA = \left| {\dfrac{{ - b}}{a}} \right|\)

(d) cắt trục Oy tại B nên \(B\left( {0;b} \right)\) suy ra \(OB = \left| b \right|\)

Diện tích \(\Delta OAB\) bằng 2 nên ta có: \(\dfrac{1}{2}.\left| b \right|.\left| {\dfrac{b}{4}} \right| = 2\)

\( \Leftrightarrow {b^2} = 2.8 = 16\)

Ta có: \(T = {a^2} + {b^2} = {4^2} + 16 = 32\)

Chọn C.

Câu 45 (NB):

Phương pháp:

Vận dụng định lí Ta – lét.

Cách giải:

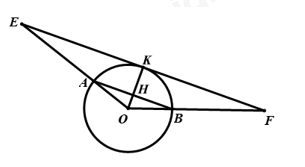
Gọi K là tiếp điểm cua đường tròn (O) với tiếp tuyến EF

H là giao điểm của OK và AB

Ta có: \(OK \bot EF\) (vì EF là tiếp tuyến của (O) tại K)

AB//EF (giả thiết)

Suy ra \(OK \bot AB\)

\( \Rightarrow H\) là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây cung)

\( \Rightarrow AH = \dfrac{1}{2}AB = \dfrac{1}{2}.24 = 12\left( {cm} \right)\)

Tam giác AOH vuông tại H, áp dụng định lý Py – ta – go, ta có:

\(\begin{array}{l}A{O^2} = A{H^2} + O{H^2}\\ \Leftrightarrow O{H^2} = A{O^2} - A{H^2}\\ \Leftrightarrow O{H^2} = {15^2} - {12^2} = 81\\ \Rightarrow OH = 9\left( {cm} \right)\end{array}\)

Tam giác OKF có HB//KF, theo Ta – lét, ta có: \(\dfrac{{OH}}{{OK}} = \dfrac{{HB}}{{KF}} = \dfrac{{OB}}{{OF}} = \dfrac{3}{5}\)

Tam giác OEF có AB//EF, theo Ta – lét, ta có: \(\dfrac{{OB}}{{OF}} = \dfrac{{AB}}{{EF}} = \dfrac{3}{5}\)

\(\begin{array}{l} \Rightarrow \dfrac{{24}}{{EF}} = \dfrac{3}{5}\\ \Rightarrow EF = \dfrac{{24.5}}{3} = 40\,\left( {cm} \right)\end{array}\)

Chọn C.

Câu 46 (VD):

Phương pháp:

Công thức tính diện tích hình tròn, hình tam giác, hình quạt.

Cách giải:

Diện tích của nửa đường tròn đường kính AB là: \({S_1} = \pi .{\left( {\dfrac{{2\sqrt 3 }}{2}} \right)^2}:2 = \dfrac{{3\pi }}{2}\)

Trong đường tròn (O) có C là điểm chính giữa cung AB nên CA = CB

Lại có C thuộc đường tròn (O) nên \(\angle ACB = {90^0}\)

Do đó, tam giác ABC vuông cân tại C, theo định lí Py – ta – go, ta có:

\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2}\\ \Leftrightarrow A{B^2} = A{C^2} + A{C^2} = 2A{C^2}\\ \Leftrightarrow {\left( {2\sqrt 3 } \right)^2} = 2A{C^2}\\ \Rightarrow AC = \sqrt 6 \end{array}\)

Diện tích quạt \({S_{qCAB}} = \dfrac{{\pi .{{\left( {\sqrt 6 } \right)}^2}.90}}{{360}} = \dfrac{3}{2}\pi \)

Diện tích tam giác ABC là: \({S_{\Delta ABC}} = \dfrac{1}{2}.\sqrt 6 .\sqrt 6  = 3\)

Diện tích phần gạch chéo là: \(\dfrac{{3\pi }}{2} - \left( {\dfrac{{3\pi }}{2} - 3} \right) = 3\,\left( {c{m^2}} \right)\)

Chọn D.

Câu 47 (VD):

Phương pháp:

Phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)

Vận dụng phương pháp tìm ước số để tìm nghiệm nguyên của phương trình.

Cách giải:

Ta có: \(\Delta ' = {\left( { - m} \right)^2} - \left( {2m - 2} \right)\)

\(\begin{array}{l} = {m^2} - 2m + 2\\ = \left( {{m^2} - 2m + 1} \right) + 1\end{array}\)

\( = {\left( {m - 1} \right)^2} + 1 > 0\) với mọi m

\( \Rightarrow \) Phương trình luôn có 2 nghiệm phân biệt với mọi m

Theo Vi – ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = 2m - 3\end{array} \right.\)

\(\begin{array}{l} \Rightarrow \left( {{x_1} + {x_2}} \right) - {x_1}{x_2} = 3\\ \Leftrightarrow {x_1} - 1 + {x_2} - {x_1}{x_2} = 2\\ \Leftrightarrow \left( {{x_1} - 1} \right) + {x_2}\left( {1 - {x_1}} \right) = 2\\ \Leftrightarrow \left( {{x_1} - 1} \right)\left( {1 - {x_2}} \right) = 2\\ \Leftrightarrow \left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) =  - 2\end{array}\)

Để phương trình có hai nghiệm nguyên thì \(\left\{ \begin{array}{l}{x_1} - 1 = 1\\{x_2} - 1 =  - 2\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}{x_1} - 1 =  - 1\\{x_2} - 1 = 2\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}{x_1} = 2\\{x_2} =  - 1\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}{x_1} = 0\\{x_2} = 3\end{array} \right.\)

Khi \({x_1} = 2,{x_2} =  - 1\) suy ra \({x_1} + {x_2} = 2 + \left( { - 1} \right) = 2m\)

\(\begin{array}{l} \Leftrightarrow 1 = 2m\\ \Leftrightarrow m = \dfrac{1}{2}\end{array}\)

Khi \({x_1} = 0,{x_2} = 3\) suy ra \({x_1} + {x_2} = 0 + 3 = 2m\)

\(\begin{array}{l} \Leftrightarrow 3 = 2m\\ \Leftrightarrow m = \dfrac{3}{2}\end{array}\)

Vậy \(m \in \left\{ {\dfrac{1}{2};\dfrac{3}{2}} \right\}\)

Suy ra có 2 giá trị của m thỏa mãn.

Chọn C.

Câu 48 (VD):

Phương pháp:

Gọi I là hình chiếu vuông góc của B trên CH (I thuộc CH)

Đặt CI = x

BI = AH, giải phương trình tìm x suy ra CH

Cách giải:

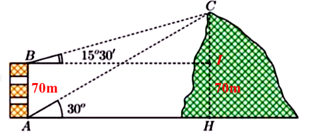
Gọi I là hình chiếu vuông góc của B trên CH (I thuộc CH)

Khi đó, tứ giác ABIH là hình chữ nhật suy ra AB = HI = 70m; AH = BI

Đặt CI = x

Tam giác BIC vuông tại I, áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có:

\(\cot \angle CBI = \dfrac{{BI}}{{CI}} \Rightarrow BI = CI.\cot \angle CBI = x.\cot {15^0}30'\)

Tam giác AHC vuông tại H, áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có:

\(\cot \angle CAH = \dfrac{{AH}}{{CH}} \Rightarrow AH = CH.\cot \angle CAH = \left( {x + 70} \right).\cot {30^0}\)

Vì AH = BI (cmt) nên ta có: \(x.\cot {15^0}30' = \left( {x + 70} \right).\cot {30^0}\)

\(\begin{array}{l} \Leftrightarrow x.\cot {15^0}30' = x.\cot {30^0} + 70.\cot {30^0}\\ \Leftrightarrow x.\left( {\cot {{15}^0}30' - \cot {{30}^0}} \right) = 70.\cot {30^0}\\ \Leftrightarrow x = \dfrac{{70.\cot {{30}^0}}}{{\cot {{15}^0}30' - \cot {{30}^0}}} \approx 64,7\,\left( {cm} \right)\end{array}\)

Khi đó, CH = 64,7 + 70 = 134,7 (cm)

Chọn C.

Câu 49 (VDC):

Phương pháp:

\(\Delta NCM \sim \Delta NPC\left( {g.g} \right)\)\( \Rightarrow N{C^2} = NP.MN\)\( \Rightarrow NC\)

Cách giải:

+ ABCD là hình bình hành nên AB//CD suy ra

\(\angle ABD = \angle BDC\) (hai góc so le trong) hay \(\angle PBN = \angle NDC\)

\(\angle ADB = \angle CBD\) (hai góc so le trong) hay \(\angle MDN = \angle NBC\)

+ Tứ giác MNCD có: \(\angle DMN = \angle DNC = {90^0}\) mà hai góc này có hai đỉnh kề nhau cùng nhìn DC dưới một góc không đổi.

Suy ra, tứ giác MNCD nội tiếp (dhnb)

\( \Rightarrow \angle NMC = \angle NDC\) (hai góc nội tiếp cùng chắn cung NC)   (1)

\(\angle MDN = \angle MCN\) (hai góc nội tiếp cùng chắn cung MN)   (2)

+ Tứ giác BCNP có: \(\angle BNC = \angle BPC = {90^0}\) mà hai góc này có hai đỉnh kè nhau cùng nhìn BC dưới một góc không đổi.

Suy ra, tứ giác BCNP nội tiếp (dhnb)

\( \Rightarrow \angle NPB = \angle NCP\) (hai góc nội tiếp cùng chắn cung NP)    (3)

\(\angle NPC = \angle NBC\) (hai góc nội tiếp cùng chắn cung NC)   (4)

Từ (1), (3) và \(\angle PBN = \angle NDC\) suy ra \(\angle NMC = \angle NCP\)

Từ (2), (4) và \(\angle MDN = \angle NBC\) suy ra \(\angle NMC = \angle NCP\)

Xét \(\Delta NCM\) và \(\Delta NPC\) có:

\(\left. \begin{array}{l}\angle NMC = \angle NCP\left( {cmt} \right)\\\angle NMC = \angle NCP\,\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta NCM \sim \Delta NPC\left( {g.g} \right)\)

\(\begin{array}{l} \Rightarrow \dfrac{{NC}}{{NP}} = \dfrac{{NM}}{{NC}}\\ \Rightarrow N{C^2} = NP.MN = 4.5 = 20\\ \Rightarrow NC = \sqrt {20}  \approx 4,47\end{array}\)

Chọn A.

Câu 50 (VDC):

Phương pháp:

Vận dụng bất đẳng thức Cô – si.

Cách giải:

\(x\sqrt {1 - {y^2}}  + y\sqrt {1 - {z^2}}  + z\sqrt {1 - {x^2}}  = \dfrac{3}{2}\)

\( \Leftrightarrow 2x\sqrt {1 - {y^2}}  + 2y\sqrt {1 - {z^2}}  + 2z\sqrt {1 - {x^2}}  = 3\)

Áp dụng bất đẳng thức Cô – si, ta có:

\(\left. \begin{array}{l}2x\sqrt {1 - {y^2}}  \le {x^2} + 1 - {y^2}\\2y\sqrt {1 - {z^2}}  \le {y^2} + 1 - {z^2}\\2z\sqrt {1 - {x^2}}  \le {z^2} + 1 - {x^2}\end{array} \right\} \Rightarrow 2x\sqrt {1 - {y^2}}  + 2y\sqrt {1 - {z^2}}  + 2z\sqrt {1 - {x^2}}  \le 3\)

Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x = \sqrt {1 - {y^2}} \\y = \sqrt {1 - {z^2}} \\z = \sqrt {1 - {x^2}} \end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x^2} = 1 - {y^2}\\{y^2} = 1 - {z^2}\\{z^2} = 1 - {x^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{y^2} = 1 - {x^2}\\{y^2} = 1 - {z^2}\end{array} \right.\)

\(\begin{array}{l} \Rightarrow 1 - {x^2} = 1 - {z^2}\\ \Rightarrow {x^2} = {z^2}\\ \Rightarrow x = z\,\left( {do\,\,\,x,y,z > 0} \right)\end{array}\)

Tương tự: \(x = y \Rightarrow x = y = z\)

Khi đó, ta có: \(2x\sqrt {1 - {x^2}}  + 2x\sqrt {1 - {x^2}}  + 2x\sqrt {1 - {x^2}}  = 3\)

\(\begin{array}{l} \Leftrightarrow 6x\sqrt {1 - {x^2}}  = 3\\ \Leftrightarrow 2x\sqrt {1 - {x^2}}  = 1\\ \Leftrightarrow 4{x^2}\left( {1 - {x^2}} \right) = 1\\ \Leftrightarrow  - 4{x^4} + 4{x^2} - 1 = 0\\ \Leftrightarrow 4{x^4} - 4{x^2} + 1 = 0\\ \Leftrightarrow {\left( {2{x^2} - 1} \right)^2} = 0\\ \Leftrightarrow 2{x^2} - 1 = 0\\ \Leftrightarrow 2{x^2} = 1\\ \Leftrightarrow {x^2} = \dfrac{1}{2}\\ \Rightarrow x = \dfrac{1}{2}\,\left( {do\,\,x > 0} \right)\\ \Rightarrow x = y = z = \dfrac{{\sqrt 2 }}{2}\end{array}\)

Khi đó, \(P = 3.{\left( {\dfrac{{\sqrt 2 }}{2}} \right)^4} = \dfrac{3}{4}\)

Chọn C.