Đề thi vào lớp 6 môn Toán trường Ngôi Sao 2023 có đáp án — Không quảng cáo

Đề bài

ĐỀ THI HỌC BỔNG NGÔI SAO MÔN TOÁN VÀO LỚP 6 TRƯỜNG NGÔI SAO HÀ NỘI

NĂM HỌC 2023 – 2024

Thời gian làm bài: 60 phút

P HẦN 1. TRẮC NGHIỆM

Câu 1. Tìm giá trị của chữ số 5 trong số 2756,29.

Câu 2. Tính \(2\frac{4}{9} + 6\frac{7}{{11}} + 7\frac{5}{9} + 13\frac{4}{{11}}\)

Câu 3. Một đơn vị bộ đội chuẩn bị lương thực đủ cho 50 người ăn trong 30 ngày. Trên thực tế, đã có 20 người chuyển sang đơn vị khác. Hỏi với số lượng thực tế đã chuẩn bị như ban đầu, đơn vị bộ đội đó sẽ đủ ăn trong bao nhiêu ngày? (Biết mức ăn của mỗi người là như nhau).

Câu 4. Câu lạc bộ World’s Scholar Cup của trường có 60 học sinh, trong đó có 10% là học sinh nam. Sau đó, có một số học sinh nữ đăng ký thêm vào câu lạc bộ nên số học sinh nam lúc này chỉ chiếm 8%. Hỏi có bao nhiêu học sinh nữ đã đăng ký thêm?

Câu 5. Mẹ mua hai bó hoa hồng và hoa cúc có số lượng bằng nhau, sau đó mẹ mua thêm 5 bông hoa hồng và 3 bông hoa cúc nên số hoa hồng bằng 51% tổng số hoa mẹ đã mua Hỏi mẹ đã mua tất cả bao nhiêu bông hoa?

Câu 6. Bố mua hai đôi giày tặng Khánh nhưng đều bị nhỏ nên bố quyết định bán hai đôi giày đã mua. Mỗi đôi bố đều bán với giá 1 500 000 đồng, trong đó, một đôi giày bố bán được nhiều hơn 20% giá mua, đôi thứ hai được ít hơn 20% giá mua. Hỏi bố Khánh đã có lãi hay bị lỗ, số tiền lãi lỗ là bao nhiêu?

Câu 7. Hình vẽ dưới đây được tạo từ các hình tam giác đều bằng nhau. Biết diện tích của hình tam giác đều nhỏ nhất là 2 cm ² . Tính diện tích hình tô đậm.

Câu 8. Trường Ngôi Sao Hà Nội 2 dự định mở cuộc thi chạy “Vì nụ cười trẻ thơ”. Các vận động viên chạy xung quanh một khu đất hình chữ nhật có chiều dài và chiều rộng lần lượt là 100 m và 65 m. Đường chạy được chia thành nhiều chặng mỗi chặng dài 75 m. Biết điểm xuất phát và kết thúc cùng một chỗ. Hỏi đường chạy có ít nhất mấy chặng?

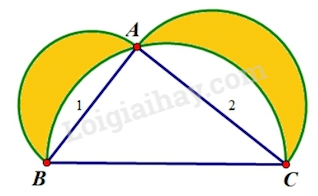
Câu 9. Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm, BC = 10 cm và ba nửa hình tròn có đường kính lần lượt là AB, AC và BC (như hình dưới đây). Tính diện tích phần tô đậm.

Câu 10. Một đoạn mật mã gồm 4 chữ số, biết tổng và hiệu của hai số được lập từ hai chữ số đầu và hai chữ số cuối đều chia hết cho 14. Hỏi phải thử ít nhất bao nhiêu lần để chắc chắn mở được đoạn mật mã này? (chẳng hạn 1428 thì 14 + 28 và 28 – 14 đều chia hết cho 14).

P HẦN 2. TỰ LUẬN

Câu 1. Tính giá trị biểu thức (4,17 + 8,77) – (3,17 – 2,23)

Câu 2. Tìm $x$ biết $x \times 7 - 6 = 0,3$

Câu 3. Trong kho có ba thùng dầu. Thùng thứ nhất đựng 28,5 lít dầu, thùng thứ hai đựng nhiều hơn thùng thứ nhất 12,3 lít dầu nhưng ít hơn thùng thứ ba 3,6 lít dầu. Hỏi trung bình mỗi thùng đựng được bao nhiêu lít dầu?

Câu 4. Cho tam giác ABC có BC = 6 cm. Trên cạnh BC lấy điểm D cách C là 2 cm. Nối A với D được tam giác ADC có diện tích bằng 4 cm ² .

a) Tinh diện tích tam giác ABC.

b) Lấy điểm E trên AB sao cho ACDE là hình thang. Tính diện tích tam giác BDE.

Câu 5. Cho ba đống sỏi gồm 7, 33 và 65 viên. Trong mỗi bước, chọn một trong hai thao tác sau để thực hiện:

• Thao tác 01: Dồn hai đống tùy ý thành một đống.
• Thao tác 02: Chọn một đống tùy ý có số chẵn viên sỏi để chia thành hai đống có số lượng viên sỏi bằng nhau.

Hỏi có khi nào nhận được 105 đống mà mỗi đống chỉ có một viên sỏi không? Vì sao?

Đáp án

HƯỚNG DẪN GIẢI CHI TIẾT

P HẦN 1. TRẮC NGHIỆM

Câu 1. Tìm giá trị của chữ số 5 trong số 2756,29.

Cách giải:

Chữ số 5 trong số 2756,29 có giá trị là 50.

Câu 2. Tính \(2\frac{4}{9} + 6\frac{7}{{11}} + 7\frac{5}{9} + 13\frac{4}{{11}}\)

Cách giải:

\(2\frac{4}{9} + 6\frac{7}{{11}} + 7\frac{5}{9} + 13\frac{4}{{11}}\)

$ = (2 + 6 + 7 + 13) + \left( {\frac{4}{9} + \frac{7}{{11}} + \frac{5}{9} + \frac{4}{{11}}} \right)$

$ = 28 + \left( {\frac{4}{9} + \frac{5}{9} + \frac{7}{{11}} + \frac{4}{{11}}} \right)$

$ = 28 + \left( {\frac{9}{9} + \frac{{11}}{{11}}} \right)$

= 28 + (1 + 1)

= 30

Câu 3. Một đơn vị bộ đội chuẩn bị lương thực đủ cho 50 người ăn trong 30 ngày. Trên thực tế, đã có 20 người chuyển sang đơn vị khác. Hỏi với số lượng thực tế đã chuẩn bị như ban đầu, đơn vị bộ đội đó sẽ đủ ăn trong bao nhiêu ngày? (Biết mức ăn của mỗi người là như nhau).

Cách giải:

Coi lượng lương thực mỗi người ăn trong 1 ngày là 1 suất thì tổng số suất chuẩn bị ban đầu là:

50 x 30 = 1500 (suất)

Sau khi chuyển đi thì số người còn lại là:

50 – 20 = 30 (người)

Với số lương thực đã chuẩn bị như ban đầu, đơn vị bộ đội sẽ đủ ăn trong số ngày là:

1500 : 30 = 50 (ngày)

Đáp số: 50 ngày

Câu 4. Câu lạc bộ World’s Scholar Cup của trường có 60 học sinh, trong đó có 10% là học sinh nam. Sau đó, có một số học sinh nữ đăng ký thêm vào câu lạc bộ nên số học sinh nam lúc này chỉ chiếm 8%. Hỏi có bao nhiêu học sinh nữ đã đăng ký thêm?

Cách giải:

Số học sinh nam ban đầu là:

60 x 10 : 100 = 6 (học sinh)

Sau đó có thêm học sinh nữ đăng kí nên số học sinh nam không thay đổi

6 học sinh nam ứng với 8% tổng số học sinh trong câu lạc bộ lúc sau.

Số học sinh trong câu lạc bộ lúc sau khi có thêm học sinh nữ đăng kí là:

6 : 8 x 100 = 75 (học sinh)

Vậy số học sinh nữ đăng kí thêm vào câu lạc bộ là:

75 – 60 = 15 (học sinh)

Đáp số: 15 học sinh

Câu 5. Mẹ mua hai bó hoa hồng và hoa cúc có số lượng bằng nhau, sau đó mẹ mua thêm 5 bông hoa hồng và 3 bông hoa cúc nên số hoa hồng bằng 51% tổng số hoa mẹ đã mua Hỏi mẹ đã mua tất cả bao nhiêu bông hoa?

Cách giải:

Số bông hoa cúc lúc sau chiếm số phần trăm là:

100% - 51% = 49% (tổng số hoa lúc sau)

Số bông hoa hồng lúc sau nhiều hơn số bông hoa cúc lúc sau là:

5 – 3 = 2 (bông hoa)

2 bông hoa chiếm số phần trăm là:

51% - 49% = 2% (tổng số hoa lúc sau)

Tổng số hoa mẹ đã mua là:

2 : 2 x 100 = 100 (bông hoa)

Đáp số: 100 bông hoa

Câu 6. Bố mua hai đôi giày tặng Khánh nhưng đều bị nhỏ nên bố quyết định bán hai đôi giày đã mua. Mỗi đôi bố đều bán với giá 1 500 000 đồng, trong đó, một đôi giày bố bán được nhiều hơn 20% giá mua, đôi thứ hai được ít hơn 20% giá mua. Hỏi bố Khánh đã có lãi hay bị lỗ, số tiền lãi lỗ là bao nhiêu?

Cách giải:

Tổng số tiền bán giày là:

1 500 000 x 2 = 3 000 000 (đồng)

Đôi giày thứ nhất bán được nhiều hơn 20% giá mua tức là bằng 120% giá mua.

Đôi thứ hai được ít hơn 20% giá mua tức là bằng 80% giá mua.

Bố mua đôi giày thứ nhất hết số tiền là:

1 500 000 : 120 x 100 = 1 250 000 (đồng)

Bố mua đôi giày thứ hai hết số tiền là:

1 500 000 : 80 x 100 = 1 875 000 (đồng)

Tổng số tiền bố mua giày là:

1 250 000 + 1 875 000 = 3 125 000 (đồng)

Vậy bố Khánh bị lỗ số tiền là:

3 125 000 – 3 000 000 = 125 000 (đồng)

Đáp số: 125 000 đồng

Câu 7. Hình vẽ dưới đây được tạo từ các hình tam giác đều bằng nhau. Biết diện tích của hình tam giác đều nhỏ nhất là 2 cm ² . Tính diện tích hình tô đậm.

Cách giải:

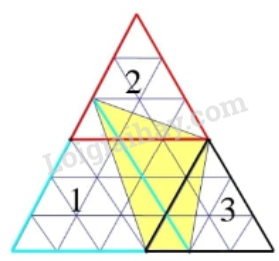
Hình tam giác to gồm 36 hình tam giác có diện tích 2 cm ² .

Ta thấy hình số 1 bao gồm 9 tam giác nhỏ và 1 phần tam giác bằng 1 nửa hình được tạo bởi 6 tam giác nhỏ nên diện tích là:

2 x 9 + 2 x 6 : 2 = 24 (cm ² )

Hình số 2 bao gồm 4 tam giác nhỏ và 1 phần tam giác bằng 1 nửa hình được tạo bởi 4 tam giác nhỏ nên diện tích là:

2 x 4 + 2 x 4 : 2 = 12 (cm ² )

Hình số 3 bao gồm 4 tam giác nhỏ và 1 phần tam giác bằng 1 nửa hình được tạo bởi 4 tam giác nhỏ nên diện tích là:

2 x 4 + 2 x 4 : 2 = 12 (cm ² )

Diện tích hình tô đậm là:

72 – 24 – 12 – 12 = 24 (cm ² )

Đáp số: 24 cm ²

Câu 8. Trường Ngôi Sao Hà Nội 2 dự định mở cuộc thi chạy “Vì nụ cười trẻ thơ”. Các vận động viên chạy xung quanh một khu đất hình chữ nhật có chiều dài và chiều rộng lần lượt là 100 m và 65 m. Đường chạy được chia thành nhiều chặng mỗi chặng dài 75 m. Biết điểm xuất phát và kết thúc cùng một chỗ. Hỏi đường chạy có ít nhất mấy chặng?

Cách giải:

Chu vi khu đất là:

(100 + 65) x 2 = 330 (m)

Vì mỗi chặng có chiều dài là 75 m nên độ dài đường chạy sẽ là:

75 x số chặng (m)

Do điểm xuất phát và kết thúc ở cùng một chỗ nên tổng độ dài số chặng phải chia hết cho chu vi của khu đất.

Khi đó ta có: (75 x số chặng) chia hết cho 330

Mà $\frac{{75}}{{330}} = \frac{5}{{22}}$

Vậy đường chạy phải có ít nhất 22 chặng.

Câu 9. Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm, BC = 10 cm và ba nửa hình tròn có đường kính lần lượt là AB, AC và BC (như hình dưới đây). Tính diện tích phần tô đậm.

Cách giải:

Diện tích nửa hình tròn đường kính BC là:

[(10 : 2) x (10 : 2) x 3,14] : 2 = 39,25 (cm ² )

Diện tích nửa hình tròn đường kính AB là:

[(6 : 2) x (6 : 2) x 3,14] : 2 = 14,13 (cm ² )

Diện tích nửa hình tròn đường kính AC là:

[(8 : 2) x (8 : 2) x 3,14] : 2 = 25,12 (cm ² )

Diện tích tam giác ABC là:

6 x 8 : 2 = 24 (cm ² )

Diện tích phần tô đậm là:

24 + 25,12 + 14,13 – 39,25 = 24 (cm ² )

Đáp số: 24 cm ²

Câu 10. Một đoạn mật mã gồm 4 chữ số, biết tổng và hiệu của hai số được lập từ hai chữ số đầu và hai chữ số cuối đều chia hết cho 14. Hỏi phải thử ít nhất bao nhiêu lần để chắc chắn mở được đoạn mật mã này? (chẳng hạn 1428 thì 14 + 28 và 28 – 14 đều chia hết cho 14).

Cách giải:

Gọi đoạn mật mã có dạng $\overline {abcd} $ trong đó $\overline {ab}  - \overline {cd} $ và $\overline {ab}  + \overline {cd} $ đều chia hết cho 14.

Điều này có nghĩa là $\overline {ab} $, $\overline {cd} $ phải cùng chia hết cho 7 và cùng tính chẵn lẻ

Trường hợp 1 : $\overline {ab} $, $\overline {cd} $ cùng chia hết cho 7 và cùng chẵn

Khi đó $\overline {ab} $ , $\overline {cd} $ sẽ nhận 2 trong các giá trị: 00, 14, 28, 42, 56, 70, 84, 98

Vì $\overline {ab} $ , $\overline {cd} $ có thể nhận giá trị bằng nhau nên có thể tạo ra số mật mã từ trường hợp này là:

8 x 8 = 64 (mật mã)

Trường hợp 2 : $\overline {ab} $, $\overline {cd} $ cùng chia hết cho 7 và cùng lẻ

Khi đó $\overline {ab} $ , $\overline {cd} $ sẽ nhận 2 trong các giá trị: 07 , 21 , 35 , 49 , 63 , 77, 91.

Vì $\overline {ab} $ , $\overline {cd} $ có thể nhận giá trị bằng nhau nên có thể tạo ra số mật mã từ trường hợp này là:

7 x 7 = 49 (mật mã)

Tổng số mật mã có thể tạo ra từ 2 trường hợp trên là:

64 + 49 = 113 (mật mã)

Vì vậy cần thử ít nhất 113 lần để chắc chắn mở được đoạn mật mã.

PHẦN 2. TỰ LUẬN

Câu 1. Tính giá trị biểu thức (4,17 + 8,77) – (3,17 – 2,23)

Cách giải:

(4,17 + 8,77) – (3,17 – 2,23)

= 4,17 + 8,77 – 3,17 + 2,23

= (4,17 – 3,17) + (8,77 + 2,23)

= 1 + 11

= 12

Câu 2. Tìm $x$ biết $x \times 7 - 6 = 0,3$

Cách giải:

$x \times 7 - 6 = 0,3$

$x \times 7 = 0,3 + 6$

$x \times 7 = 6,3$

$x = 6,3:7$

$x = 0,9$

Câu 3. Trong kho có ba thùng dầu. Thùng thứ nhất đựng 28,5 lít dầu, thùng thứ hai đựng nhiều hơn thùng thứ nhất 12,3 lít dầu nhưng ít hơn thùng thứ ba 3,6 lít dầu. Hỏi trung bình mỗi thùng đựng được bao nhiêu lít dầu?

Cách giải:

Thùng thứ hai đựng được số lít dầu là:

28,5 + 12,3 = 40,8 (lít dầu)

Thùng thứ ba đựng được số lít dầu là:

40,8 + 3,6 = 44,4 (lít dầu)

Trung bình mỗi thùng đựng được số lít dầu là:

(28,5 + 40,8 + 44,4) : 3 = 37,9 (lít dầu)

Đáp số: 37,9 lít dầu

Câu 4. Cho tam giác ABC có BC = 6 cm. Trên cạnh BC lấy điểm D cách C là 2 cm. Nối A với D được tam giác ADC có diện tích bằng 4 cm ² .

a) Tinh diện tích tam giác ABC.

b) Lấy điểm E trên AB sao cho ACDE là hình thang. Tính diện tích tam giác BDE.

Cách giải

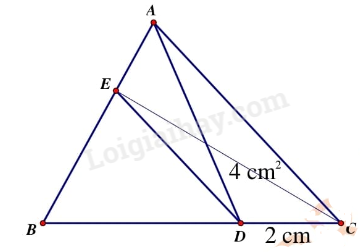
a) Ta có:

Xét tam giác ADC và tam giác ABC có chung chiều cao hạ từ đỉnh A xuống BC:

Nên $\frac{{{S_{ADC}}}}{{{S_{ABC}}}} = \frac{{DC}}{{BC}} = \frac{2}{6} = \frac{1}{3}$

Vậy S _ABC = 3 x S _ADC = 3 x 4 = 12 (cm ² )

b) Nối E với C

S _AEC = S _ADC = 4 (cm ² ) (Vì chung đáy AC, chiều cao hạ từ đỉnh E xuống AC bằng chiều cao hạ từ đỉnh D xuống đáy AC)

S _EBC = S _ABC – S _AEC = 12 – 4 = 8 (cm ² )

$\frac{{{S_{EBD}}}}{{{S_{EBC}}}} = \frac{{BD}}{{BC}} = \frac{4}{6} = \frac{2}{3}$ (Hai tam giác có chung chiều cao hạ từ E xuống BC)

Suy ra S _EBD = $\frac{2}{3}$ x S _EBC = $\frac{2}{3} \times 8$ = $\frac{{16}}{3}$ (cm ² )

Câu 5. Cho ba đống sỏi gồm 7, 33 và 65 viên. Trong mỗi bước, chọn một trong hai thao tác sau để thực hiện:

• Thao tác 01: Dồn hai đống tùy ý thành một đống.
• Thao tác 02: Chọn một đống tùy ý có số chẵn viên sỏi để chia thành hai đống có số lượng viên sỏi bằng nhau.

Hỏi có khi nào nhận được 105 đống mà mỗi đống chỉ có một viên sỏi không? Vì sao?

Cách giải:

Vì 7, 33 và 65 đều lẻ nên bước đầu tiên ta chỉ có thao tác 1 là dồn hai đống tùy ý thành một đống.

- Trường hợp 1: Dồn 2 đống 7 ; 33 dồn thành đống 40, khi đó ta được hai đống 40 ; 65

Nhận xét rằng số sỏi chia hết cho 5 nên các thao tác sau dù chia đôi hay gộp lại cũng sẽ tạo ra kết quả là số sỏi chia hết cho 5 nên không thể xảy ra trường hợp mỗi đống 1 viên.

- Trường hợp 2: Dồn 2 đống 7 ; 65 dồn thành đống 72, khi đó ta được hai đống 33 ; 72

Nhận xét rằng số sỏi chia hết cho 3 nên các thao tác sau dù chia đôi hay gộp lãi cũng sẽ tạo ra kết quả là số sỏi chia hết cho 3 nên không thể xảy ra trường hợp mỗi đống 1 viên.

- Trường hợp 3: Dồn 2 đống 33 ; 65 dồn thành đống 98, khi đó ta được hai đống 7 ; 98

Nhận xét rằng số sỏi chia hết cho 7 nên các thao tác sau dù chia đôi hay gộp lãi cũng sẽ tạo ra kết quả là số sỏi chia hết cho 7 nên không thể xảy ra trường hợp mỗi đống 1 viên.

Vậy không thể nhận được 105 đống mà mỗi đống chỉ có một viên sỏi.