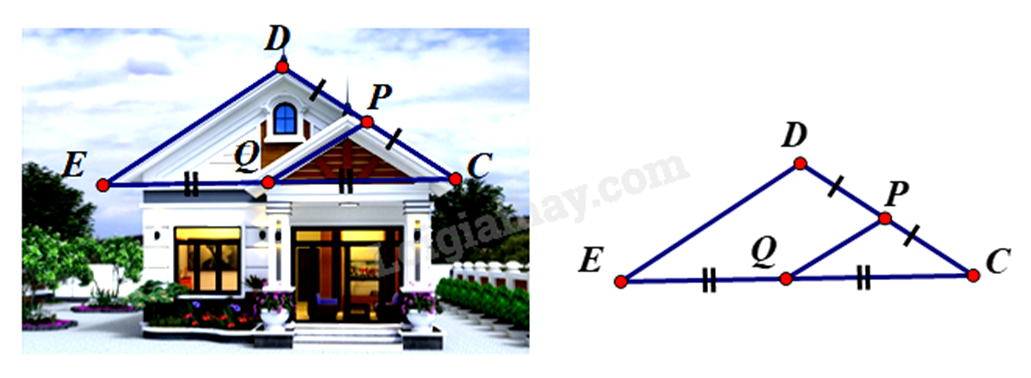
1. Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Em hãy tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa) ?
2. Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Gọi M và N theo thứ tự là trung điểm của các đoạn AH và DH.
a) Chứng minh MN//AD.
b) Gọi I là trung điểm của cạnh BC. Chứng minh tứ giác BMNI là hình bình hành.
c) Chứng minh tam giác ANI vuông tại N.
1. Dựa vào tính chất của đường trung bình để tính.
2.
a) Dựa vào tính chất của đường trung bình để chứng minh.
b) Chứng mình BMNI có hai cạnh đối song song và bằng nhau.
c) Chứng minh M là trực tâm của tam giác ABN nên BM \( \bot \) AN, mà BM // NI nên AN \( \bot \) NI hay \(\widehat {ANI} = {90^0}\)=> ANI là tam giác vuông tại N.
1.
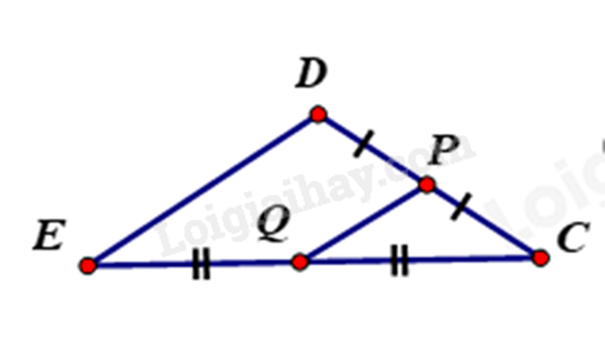
Vì Q là trung điểm EC, P là trung điểm của DC nên PQ là đường trung bình của tam giác CDE.
\(\begin{array}{l} \Rightarrow QP = \frac{1}{2}DE\\ \Rightarrow DE = 2QP = 2.1,5 = 3m\end{array}\)
Vậy chiều dài mái DE bằng 3m.
2.
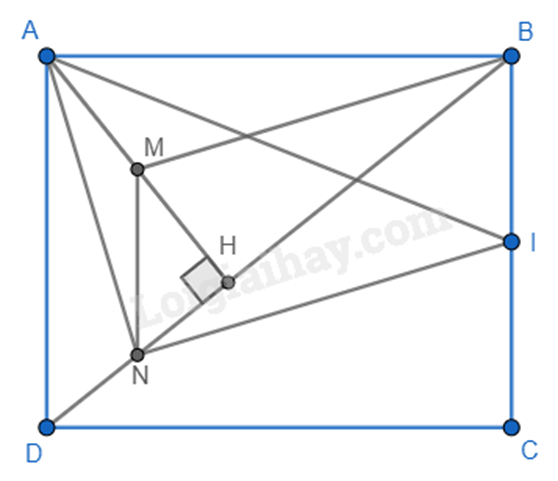
a) Ta có M là trung điểm của AH, N là trung điểm của DH nên MN là đường trung bình của tam giác ADH => MN // AD và MN = \(\frac{1}{2}\)
b) Vì ABCD là hình chữ nhật nên AD // BC và AD = BC; I là trung điểm của BC nên BI = \(\frac{1}{2}\)
=> MN // BI (cùng song song với AD) và MN = BI (= \(\frac{1}{2}\)BC = \(\frac{1}{2}\)AD). Khi đó BMNI là hình bình hành.
c) Ta có MN // AD mà AD \( \bot \) AB (ABCD là hình chữ nhật) nên MN \( \bot \) Xét tam giác ABN có AH \( \bot \) BN; MN \( \bot \) AB; AH giao MN tại N nên N là trực tâm của tam giác ABN. Suy ra BM \( \bot \) AN.
Mà BM // IN (BMNI là hình bình hành) nên AN \( \bot \) IN hay \(\widehat {ANI} = {90^0}\)=> ANI là tam giác vuông tại N.