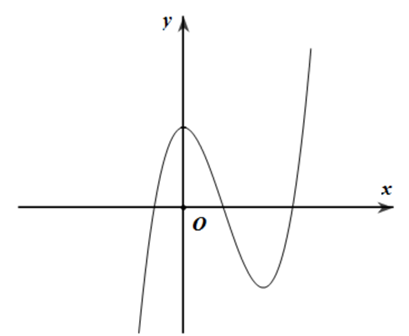
Đồ thị của hàm số nào dưới đây có dạng như trong hình — Không quảng cáo

Phương pháp giải

Quan sát đồ thị và nhận xét.

Ta có $\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty$ nên a > 0. Loại B, D.

Hàm số đạt cực trị tại ${x_1} = 0$ và ${x_2} > 0$.

Xét hàm số $y = {x^3} + 3{x^2} + 2$ có $y' = 3{x^2} + 6x = 0$ suy ra x = -2 hoặc x = 0.

Suy ra $y = {x^3} + 3{x^2} + 2$ đạt cực trị tại ${x_1} = 0$ và ${x_2} < 0$. Loại C.