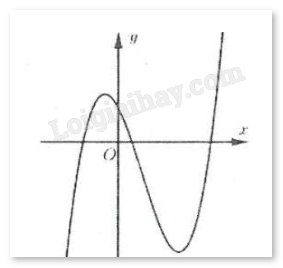
Đường cong hình bên là đồ thị của hàm số \(y = a{x^3} + b{x^2} + cx + d\) . Khẳng định nào sau đây đúng?
-
A.
a > 0, b < 0, c > 0, d > 0
-
B.
a > 0, b < 0, c < 0, d > 0
-
C.
a > 0, b > 0, c < 0, d > 0
-
D.
a < 0, b > 0, c > 0, d < 0
Dựa vào sự biến thiên và cực trị của hàm số để xét dấu.
Dựa vào đồ thị ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) nên a > 0. Loại D.
Đồ thị đi qua điểm (0;d) nên d > 0 (vì đồ thị cắt trục tung tại điểm có tung độ dương).
Hàm số đạt cực trị tại hai điểm \({x_1},{x_2}\). Dựa vào hình vẽ ta thấy \({x_1} < 0,x{}_2 > 0\) và \({x_1} + {x_2} > 0\).
Mặt khác, \(y' = 3a{x^2} + 2bx + c \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = \frac{{ - 2b}}{{3a}} > 0 \Rightarrow b < 0}\\{{x_1}{x_2} = \frac{c}{{3a}} < 0 \Rightarrow c < 0}\end{array}} \right.\)
Đáp án : B