Giá trị lớn nhất của hàm số x - 2^2. E^x trên đoạn [0;3] — Không quảng cáo

Phương pháp giải

Lập bảng biến thiên và tìm GTLN.

$y = {(x - 2)^2}.{e^x}$ có tập xác định $D = \mathbb{R}$.

$y' = 2(x - 2).{e^x} + {(x - 2)^2}.{e^x} = (x - 2).{e^x}.[2 + (x - 2)] = x.(x - 2).{e^x}$

$y' = 0$ suy ra x = 0 hoặc x = 2.

Ta có bảng biến thiên:

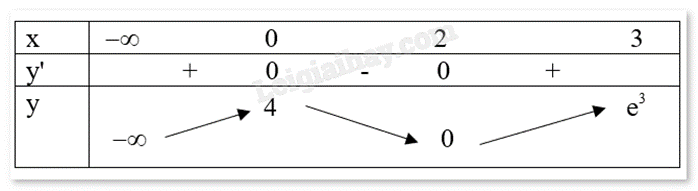
Vậy giá trị lớn nhất của hàm số ${(x - 2)^2}.{e^x}$ trên đoạn $[0;3]$ bằng ${e^3}$.