Giải bài 11 trang 77 Sách bài tậpToán 6 – Chân trời sáng tạo
Tính chu vi và diện tích của Hình 1 và tính diện tích của Hình 2 sau đây.
Đề bài
Tính chu vi và diện tích của Hình 1 và tính diện tích của Hình 2 sau đây.
Lời giải chi tiết
Hình 1:
Chu vi hình 1 là:
25 + 50 +50 + 55 = 180 (m)
Chia hình 1 thành hình gồm 1 tam giác và 1 hình thang cân như hình dưới.
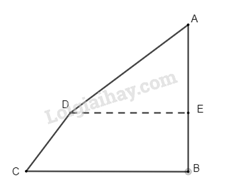
Ta có: AD = 50 m, AB = 50 m, CD = 25 m, BC = 55 m.
Từ đề bài dễ dàng suy ra BE = 20 m và DE = 40m.
\( \Rightarrow \)AE = AB – BE = 50 – 20 = 30 (m)
Diện tích tam giác ADE là: ED. AE : 2 = 40 . 30 : 2 = 600 (\({m^2}\))
Diện thích hình thang CDEB là: (DE+BC).BE:2 = (40 + 55). 20 : 2 = 950 (\({m^2}\))
Vậy diện tích Hình 1 là: 600 + 950 = 1550 (\({m^2}\))
Hình 2:
Ta chia hình 2 như sau:
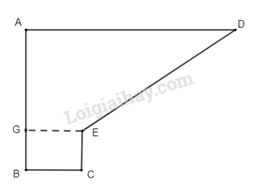
Hình gồm hình chữ nhật BCEG và hình thang ABEG.
Diện tích hình chữ nhật là: EC. BC = 40 . 60 = 2400 (\({m^2}\))
Vì EG = BC nên EG = 60 m; AG = AB – GB = AB – EC = 120 – 40 = 80 (m)
Diện tích hình thang BCEG là: (60 + 200). 80 : 2 = 10400 (\({m^2}\))
Vậy diện tích hình 2 là: 2400 + 10400 = 12800 (\({m^2}\))