Giải bài 2.25 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức
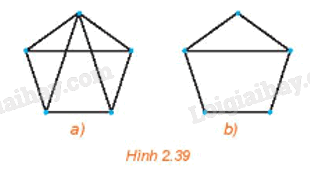
Kiểm tra xem các điều kiện của định lí Ore có thỏa mãn với các đồ thị trên Hình 2.39 không.
Đề bài
Kiểm tra xem các điều kiện của định lí Ore có thỏa mãn với các đồ thị trên Hình 2.39 không.
Phương pháp giải - Xem chi tiết
Định lí Ore: Nếu G là đơn đồ thị có n đỉnh \(\left( {n \ge 3} \right)\) và mỗi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn n thì G có một chu trình Hamilton.
Lời giải chi tiết
Ta thấy hai đồ thị ở Hình 2.39 đều là đơn đồ thị và mỗi đồ thị đều có số đỉnh lớn hơn 3.
+) Đối với Hình 2.39 a), đặt tên các đỉnh như hình vẽ:
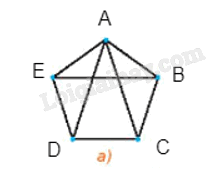
Đồ thị này có 5 đỉnh, các đỉnh đều có bậc là 3, trừ đỉnh A có bậc là 4 nên mỗi cặp đỉnh không kề nhau có tổng bậc nhỏ nhất là 6, mà 6 > 5, do đó đồ thị này thỏa mãn định lí Ore. Vậy đồ thị Hình 2.39 a) có một chu trình Hamilton.
+) Đối với Hình 2.39 a), đặt tên các đỉnh như hình vẽ:
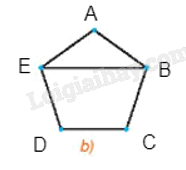
Đồ thị này có 5 đỉnh, đỉnh E và đỉnh B đều có bậc là 3, các đỉnh còn lại đều có bậc là 2 nên mỗi cặp đỉnh không kề nhau có tổng số bậc nhỏ nhất là 4 (chẳng hạn đỉnh A và đỉnh D), do đó đồ thị này không thỏa mãn định lí Ore. Tuy nhiên thì đồ thị này vẫn có chu trình Hamilton, một chu trình Hamilton của đồ thị là ABCDEA.
Do đó, ta khẳng định lại định lí Ore chỉ là một điều kiện đủ cho sự tồn tại của chu trình Hamilton.