Giải bài 2 trang 78 vở thực hành Toán 8 — Không quảng cáo

Đề bài

Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.

a) Chứng minh EK // CD, FK // AB.

b) So sánh EF và \(\frac{1}{2}\left( {AB + CD} \right).\)

Lời giải chi tiết

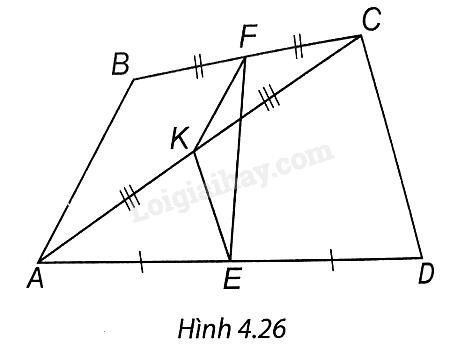
a) ∆ABC có F là trung điểm BC, K là trung điểm AC nên FK là đường trung bình của ∆ABC, suy ra FK // AB.

∆ACD có E là trung điểm AD nên EK là đường trung bình của ∆ACD, suy ra EK // CD.

b) FK là đường trung bình của ∆ABC nên AB = 2FK.

Tương tự CD = 2EK.

Ta có FK + KE ≥ FE nên \(\frac{1}{2}\left( {AB + CD} \right) \ge EF.\)

Do đó \(EF\le \;\frac{1}{2}\left( {AB + CD} \right).\)